数论分块

例题

AK训练计划

Description

AK——All Killed，当一名选手把所有的题目全部AC（Accept）时，我们称他AK了这场比赛。

AK，是每个ACM选手的梦想，而防AK，则是每个出题人应尽的义务。一般我们称一场比赛中最难的题目为防AK题。

“cy教练，我……我想打ACM！”，小萌新说道。

教练给小萌新们发布了历时 $n$ 天的AK训练计划。
在第 i 天的训练计划中，有 $[\frac{n}{i}]$ 道题目，每道题目可以给小萌新们带来 $[\sqrt{i}]$ 点经验值。 $[i]$ 表示 $i$ 的下取整）

现在，小明同学希望AK每一天的训练计划，但他想知道经过这 $n$ 天的训练后，他能得到多少经验值呢？

Input

输入仅一行，表示训练计划的天数 $n (1≤n≤10^9)$

Output

输出一行，表示 $n$ 天后小明得到的总经验值。

Sample Input 1

100

Sample Output 1

1451

时间限制                      1000 ms

内存限制                       256 MB

参考题解

注意到数据范围是$n (1≤n≤10^9)$，暴力不可行，需要用到数论分块相关知识。

• 结论：
  对于常数 $n$，使得式子

  $$\left\lfloor\dfrac ni\right\rfloor=\left\lfloor\dfrac nj\right\rfloor$$

  成立的最大的满足 $i\leq j\leq n$ 的 $j$ 的值为 $\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor$。即值 $\left\lfloor\dfrac ni\right\rfloor$ 所在的块的右端点为 $\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor$。

  详证见下文

• $\lfloor\sqrt{i}\rfloor$ 前缀和求解（时间复杂度：$O(1)$）

  对于 $g(n)$ 表示 $\Sigma_{i=1}^n\lfloor\sqrt{i}\rfloor$
  特殊处理一下值为 $\lfloor\sqrt{n}\rfloor$ 的项的和, 其和为 $\lfloor\sqrt{n}\rfloor\left(n-(\lfloor\sqrt{n}\rfloor)^2+1\right)$
  值为 1 到 $\lfloor\sqrt{n}\rfloor-1$ 的项 ( $\lfloor\sqrt{i}\rfloor$ 的其余项) 分别有 $2\lfloor\sqrt{i}\rfloor+1$ 个，其和为

  $$\Sigma_{i=1}^{\lfloor\sqrt{n}\rfloor-1}\left(2 i^2+i\right)=\frac{\lfloor\sqrt{n}\rfloor(\lfloor\sqrt{n}\rfloor-1)(2\lfloor\sqrt{n}\rfloor-1)}{3}+\frac{\lfloor\sqrt{n}\rfloor(\lfloor\sqrt{n}\rfloor-1)}{2}$$

  因此, 前缀和表达式为：

  $$g(x)=\lfloor\sqrt{x}\rfloor\left(x-(\lfloor\sqrt{x}\rfloor)^2+1\right)+\frac{\lfloor\sqrt{x}\rfloor(\lfloor\sqrt{x}\rfloor-1)(2\lfloor\sqrt{x}\rfloor-1)}{3}+\frac{\lfloor\sqrt{x}\rfloor(\lfloor\sqrt{x}\rfloor-1)}{2}$$

#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
ll getsum(ll x)
{
    ll y = sqrt(x), z = y - 1;
    return z*(z + 1)*(2*z + 1)/3 + z*(z + 1)/2 + y*(x - y*y + 1);
}
int main()
{
    ll n, s = 0;
    cin >> n;
    for (ll l = 1, r; l <= n; l = r + 1)
    {
        r = min(n / (n / l), n);
        s += (n / l)*(getsum(r) - getsum(l - 1));
    }
    cout << s;
    return 0;
}

数论分块

以下参考OI-wiki

数论分块可以快速计算一些含有除法向下取整的和式（即形如 $\sum_{i=1}^nf(i)g(\left\lfloor\dfrac ni\right\rfloor)$ 的和式）。当可以在 $O(1)$ 内计算 $f(r)-f(l)$ 或已经预处理出 $f$ 的前缀和时，数论分块就可以在 $O(\sqrt n)$ 的时间内计算上述和式的值。

它主要利用了富比尼定理（Fubini’s theorem），将 $\left\lfloor\dfrac ni\right\rfloor$ 相同的数打包同时计算。

富比尼定理

又称「算两次」，以意大利数学家圭多·富比尼（Guido Fubini）命名。
富比尼定理的积分形式：只要二重积分 $\int\int |f(x,y)|dxdy$ 有界，则可以逐次计算二重积分，并且可以交换逐次积分的顺序。
积分号也是特殊的求和号，因此在一般求和中，富比尼定理往往呈现为更换计数顺序，即交换两个求和号。
组合数学中的富比尼定理表现为，用两种不同的方法计算同一个量，从而建立相等关系。

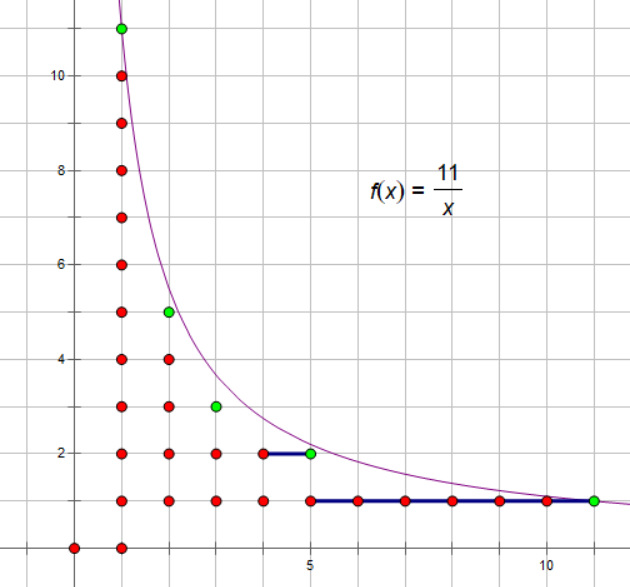
例如这里的双曲线下整点的图片：

图中共分为了 $5$ 块，这 $5$ 块整点的最大纵坐标都相同。如果统计整点的个数，可以从纵向计数改为横向计数，直接计算 $5$ 个矩形即可。

引理 1

$$\forall a,b,c\in\mathbb{Z},\left\lfloor\frac{a}{bc}\right\rfloor=\left\lfloor\frac{\left\lfloor\frac{a}{b}\right\rfloor}{c}\right\rfloor$$

略证：

$$\begin{aligned} &\frac{a}{b}=\left\lfloor\frac{a}{b}\right\rfloor+r(0\leq r<1)\\ \implies &\left\lfloor\frac{a}{bc}\right\rfloor =\left\lfloor\frac{a}{b}\cdot\frac{1}{c}\right\rfloor =\left\lfloor \frac{1}{c}\left(\left\lfloor\frac{a}{b}\right\rfloor+r\right)\right\rfloor =\left\lfloor \frac{\left\lfloor\frac{a}{b}\right\rfloor}{c} +\frac{r}{c}\right\rfloor =\left\lfloor \frac{\left\lfloor\frac{a}{b}\right\rfloor}{c}\right\rfloor\\ &&\square \end{aligned}$$

引理 2

$$\forall n \in \mathbb{N}_{+}, \left|\left\{ \lfloor \frac{n}{d} \rfloor \mid d \in \mathbb{N}_{+},d\leq n \right\}\right| \leq \lfloor 2\sqrt{n} \rfloor$$

$|V|$ 表示集合 $V$ 的元素个数

略证：

对于 $d\leq \left\lfloor\sqrt{n}\right\rfloor$，$\left\lfloor\frac{n}{d}\right\rfloor$ 有 $\left\lfloor\sqrt{n}\right\rfloor$ 种取值

对于 $d> \left\lfloor\sqrt{n}\right\rfloor$，有 $\left\lfloor\frac{n}{d}\right\rfloor\leq\left\lfloor\sqrt{n}\right\rfloor$，也只有 $\left\lfloor\sqrt{n}\right\rfloor$ 种取值

综上，得证

数论分块结论

对于常数 $n$，使得式子

$$\left\lfloor\dfrac ni\right\rfloor=\left\lfloor\dfrac nj\right\rfloor$$

成立的最大的满足 $i\leq j\leq n$ 的 $j$ 的值为 $\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor$。即值 $\left\lfloor\dfrac ni\right\rfloor$ 所在的块的右端点为 $\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor$。

证明

令 $k=\left\lfloor\dfrac ni\right\rfloor$，可以知道 $k\leq\dfrac ni$。

$$\begin{aligned}&\therefore \left\lfloor\dfrac nk\right\rfloor\geq\left\lfloor\dfrac n{\frac ni}\right\rfloor=\lfloor i\rfloor=i\\&\therefore j=\max{\text{满足条件的所有 }i}=i_{\max}=\left\lfloor\dfrac nk\right\rfloor=\left\lfloor\dfrac n{\left\lfloor\dfrac ni\right\rfloor}\right\rfloor \square\end{aligned}$$

过程

数论分块的过程大概如下：考虑和式

$\sum_{i=1}^nf(i)\left\lfloor\dfrac ni\right\rfloor$

那么由于我们可以知道 $\left\lfloor\dfrac ni\right\rfloor$ 的值成一个块状分布（就是同样的值都聚集在连续的块中），那么就可以用数论分块加速计算，降低时间复杂度。

利用上述结论，我们先求出 $f(i)$ 的 前缀和（记作 $s(i)=\sum_{j=1}^i$ f(j)），然后每次以 $[l,r]=[l,\left\lfloor\dfrac n{\lfloor\frac ni\rfloor}\right\rfloor]$ 为一块，分块求出贡献累加到结果中即可。

伪代码如下：

$$\begin{array}{ll} 1 & \text{获取 }f(i)\text{ 函数的前缀和，记为 }s(i).\\ 2 & l\gets 1\\ 3 & r\gets 0\\ 4 & result\gets 0\\ 5 & \textbf{while }l\leq n\textbf{ do}:\\ 6 & \qquad r\gets\left\lfloor\dfrac n{\lfloor\frac nl\rfloor}\right\rfloor\\ 7 & \qquad result\gets [s(r)-s(l-1)]\times\left\lfloor\dfrac nl\right\rfloor\\ 8 & \qquad l\gets r+1\\ 9 & \textbf{end while}\\ \end{array}$$

最终得到的 $result$ 即为所求的和式。

N 维数论分块

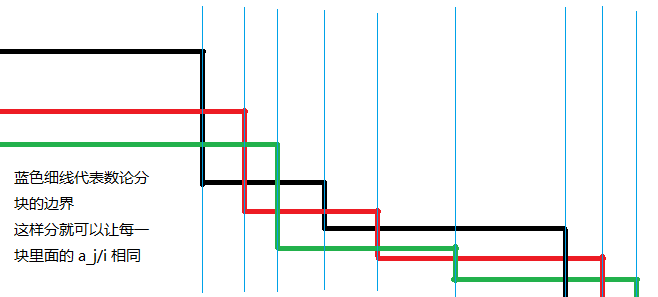
求含有 $\left\lfloor\dfrac {a_1}i\right\rfloor$、$\left\lfloor\dfrac {a_2}i\right\rfloor\cdots\left\lfloor\dfrac {a_n}i\right\rfloor$ 的和式时，数论分块右端点的表达式从一维的 $\left\lfloor\dfrac ni\right\rfloor$ 变为 $\min\limits_{j=1}^n\{\left\lfloor\dfrac {a_j}i\right\rfloor\}$，即对于每一个块的右端点取最小（最接近左端点）的那个作为整体的右端点。可以借助下图理解：

一般我们用的较多的是二维形式，此时可将代码中 r = n / (n / i) 替换成 r = min(n / (n / i), m / (m / i))。

习题

1. 1363 - Joseph’s Problem（注意有几个坑，参考洛谷）