统计计算

配套教材为 统计计算 田霞,徐瑞民,孙倩

个人思路，仅供参考

习题1.1

第1题

$$V = \frac{4}{3}\pi R^3$$

根据幂函数的误差传递规则，体积的相对误差为半径相对误差的 3 倍：

$$\frac{\Delta V}{V} = 3 \cdot \frac{\Delta R}{R}$$

已知体积的相对误差限为 1%，代入公式得：

$$3 \cdot \frac{\Delta R}{R} \leq 0.01 \implies \frac{\Delta R}{R} \leq \frac{0.01}{3} \approx 0.00333$$

测量半径 R 时允许的相对误差限为 0.00333

第3题

根据公式

$$x^*=10^m\left(a_0+a_1 \times 10^{-1}+a_2 \times 10^{-2}+\cdots+a_n \times 10^{-n}\right)$$ $$\quad\left|x-x^*\right| \leqslant \frac{1}{2} \times 10^{(m-n+1)}$$ $$a_{i} = 0, 1, 2, ... , 9，m, n 是整数，a_{0} \not= 0$$

得 m = -1 ，m - n + 1 = -5 得 n = 5 ，即有效数字有5位。

第5题

1. 绝对误差限
   $x$ 的相对误差限为 $\varepsilon$，即满足：

   $$\frac{|x^* - x|}{x} \leq \varepsilon \quad \implies \quad |\Delta x| \leq \varepsilon x$$

   其中 $x^*$ 是 $x$ 的近似值， $\Delta x = x^* - x$。

   对于函数 $f(x) = \ln x$，其一阶泰勒展开近似为：

   $$f(x^*) \approx f(x) + f'(x) \cdot \Delta x$$

   绝对误差为：

   $$|\Delta(\ln x)| \approx |f'(x)| \cdot |\Delta x| = \frac{1}{x} \cdot |\Delta x|$$

   代入 $|\Delta x| \leq \varepsilon x$ 得：

   $$|\Delta(\ln x)| \leq \frac{1}{x} \cdot \varepsilon x = \varepsilon$$

   绝对误差限为 $\varepsilon$

2. 相对误差限
   相对误差限定义为绝对误差限与函数值的绝对值之比：

   $$\text{相对误差限} = \frac{|\Delta(\ln x)|}{|\ln x^*|}$$

   代入绝对误差限 $\varepsilon$，相对误差限即 $|\frac{\varepsilon}{\ln x^*}|$

第7题

$x$ 的可能范围为： $0.17525 \leq x < 0.17535$
最大绝对误差为 $|x - x^*| < 0.5 \times 10^{-4}$
即绝对误差限为 $0.5 \times 10^{-4}$

第9题

1. 求递推公式

   写出

   $$s_{n+1} = \int_{0}^{1} \frac{x^{n+1}}{x+5}\,dx.$$

   分拆被积函数

   $$\frac{x^{n+1}}{x+5} = \frac{x^{n+1} + 5x^n - 5x^n}{x+5} = \frac{x^n(x+5) - 5x^n}{x+5} = x^n - 5\,\frac{x^n}{x+5}.$$

   因此

   $$s_{n+1} = \int_{0}^{1} x^n\,dx - 5 \int_{0}^{1} \frac{x^n}{x+5}\,dx.$$

   计算积分并代回

   $$\int_{0}^{1} x^n \,dx = \left[\frac{x^{n+1}}{n+1}\right]_{0}^{1} = \frac{1}{n+1}.$$ $$\int_{0}^{1} \frac{x^n}{x+5}\,dx = s_n.$$

   从而得到递推关系

   $$s_{n+1} = \frac{1}{n+1} - 5\,s_n.$$

   即

   $$s_{n} = \frac{1}{n} - 5\,s_{n-1}.$$ $$s_{n-1} = \frac{\frac{1}{n} - s_n}{5}$$

import sympy as sp
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='MicroSoft YaHei')

# 迭代次数
n = 10

# 定义变量和函数
x = sp.symbols('x')

# 定义表达式
expr_0 = x**0 / (x + 5)
expr_10 = x**n / (x + 5)

# 计算定积分
s_0 = round(sp.integrate(expr_0, (x, 0, 1)).evalf(), 4)
s_10 = round(sp.integrate(expr_10, (x, 0, 1)).evalf(), 4)

# 记录每次迭代的值
s_0_values = [s_0]
s_10_values = [s_10]

# 迭代计算和记录
for k in range (1, n + 1):
    s_0 = round(1 / k - 5 * s_0, 4)
    s_0_values.append(s_0)

for k in range (n, 0, -1):
    s_10 = round((1 / k - s_10) / 5, 4)
    s_10_values.append(s_10)

# 打印结果
print("s_0", s_0_values)
print("s_10", s_10_values)

# 绘制图形
plt.plot(range(n + 1), s_0_values, marker='o', linestyle='-', color='blue', label='s_0 values')
plt.plot(range(n + 1), s_10_values, marker='o', linestyle='-', color='red', label='s_10 values')
plt.title('迭代计算结果')
plt.xlabel('S(k)')
plt.ylabel('S(k)的值')
plt.grid(True)
plt.legend()
plt.show()

习题1.2

第2题

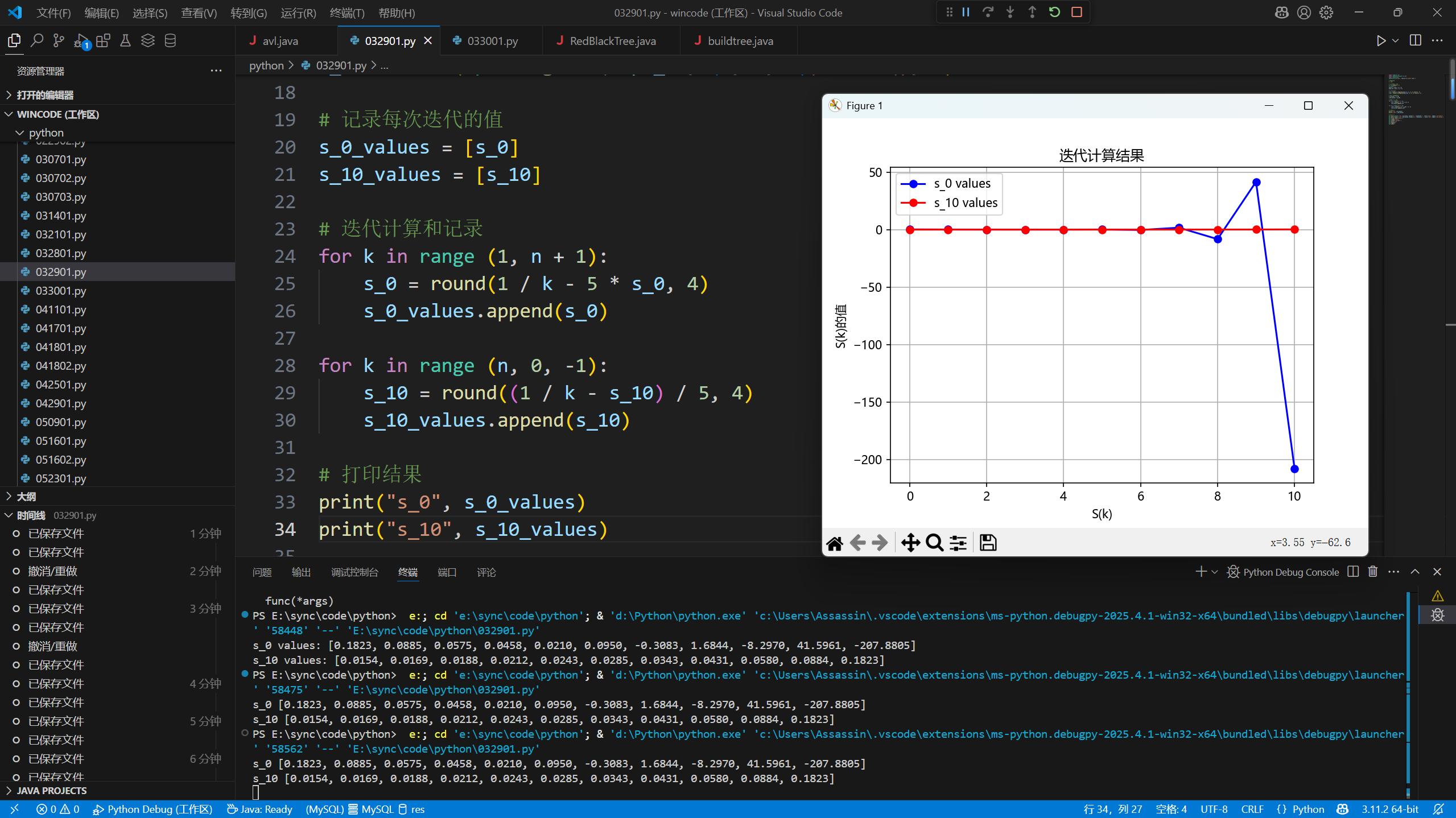
三个解
迭代值 1.879385241571822 绝对误差为 8.309744825574228e-08
迭代值 -0.347296353163868 绝对误差为 7.413094164571143e-05
迭代值 -1.5320888862414666 绝对误差为 1.757033387228546e-06

import sympy

n = 20          # 迭代次数
x0 = 1.5        # 初始值（-1.5, -0.5）

# 定义函数f(x)
def f(x):
    y = x**3 - 3 * x - 1
    return y

# 求f(x)的导数
def g(x0):
    x = sympy.symbols('x')
    y = x**3 - 3 * x - 1
    z = sympy.diff(y, x)
    # 把x0的值代入导数中
    t = float(z.evalf(subs={x: x0}))
    return t

# 用牛顿法求根
for i in range(n):
    k = x0
    s = f(k)
    t = g(k)
    x1 = k - s / t
    e = abs(x1 - x0)
    print(i + 1, '迭代值', x1, '绝对误差为', e)
    if e < 0.0001:
        break
    x0 = x1

print('函数值', s, '导数值', t)

第4题

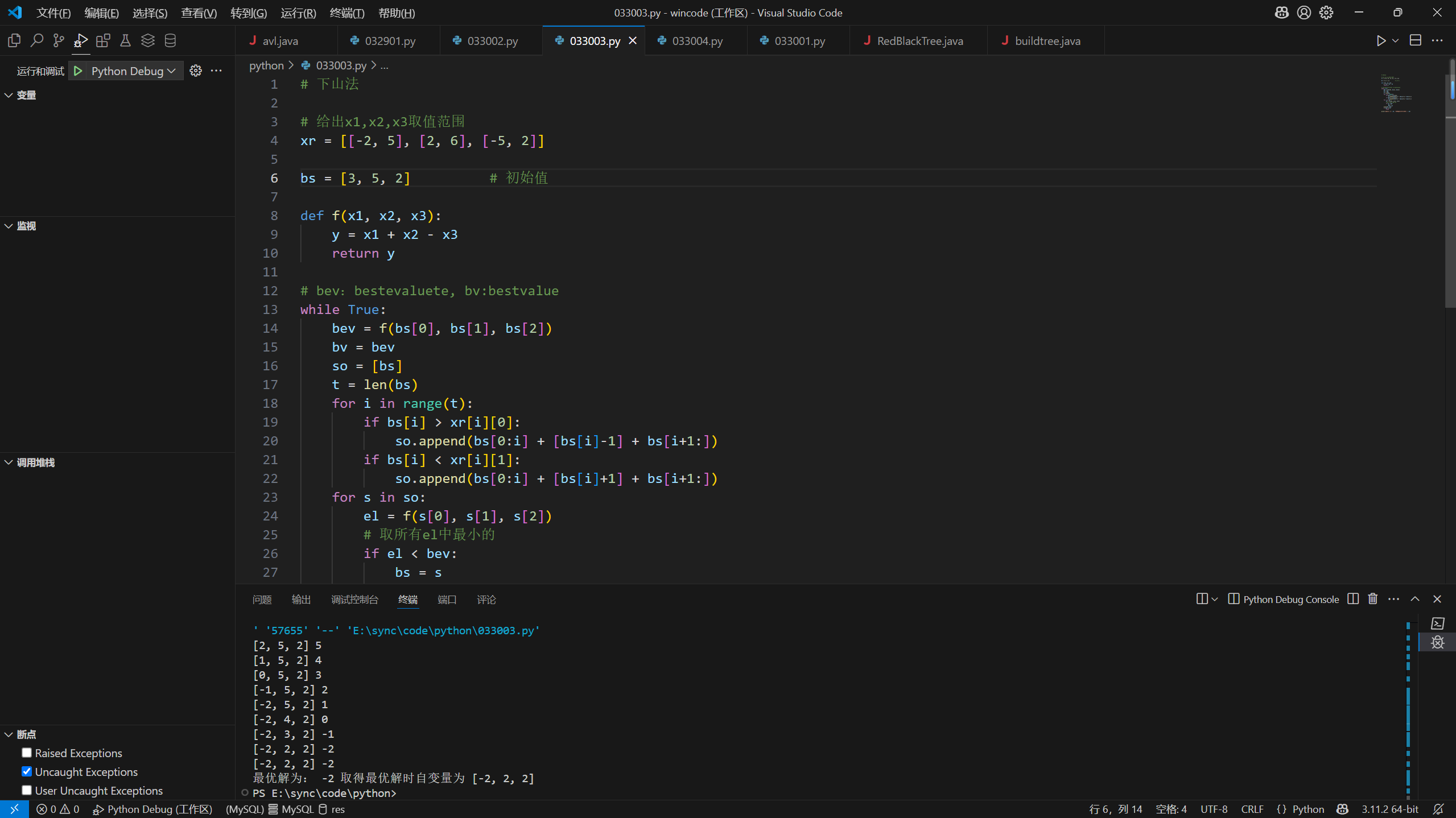
最优解为： -2 取得最优解时自变量为 [-2, 2, 2]

# 下山法

# 给出x1,x2,x3取值范围
xr = [[-2, 5], [2, 6], [-5, 2]]

bs = [3, 5, 2]          # 初始值

def f(x1, x2, x3):
    y = x1 + x2 - x3
    return y

# bev：bestevaluete, bv:bestvalue
while True:
    bev = f(bs[0], bs[1], bs[2])
    bv = bev
    so = [bs]
    t = len(bs)
    for i in range(t):
        if bs[i] > xr[i][0]:
            so.append(bs[0:i] + [bs[i]-1] + bs[i+1:])
        if bs[i] < xr[i][1]:
            so.append(bs[0:i] + [bs[i]+1] + bs[i+1:])
    for s in so:
        el = f(s[0], s[1], s[2])
        # 取所有el中最小的
        if el < bev:
            bs = s
            bev = el
    print(bs, bev)
    if bev == bv:
        break

print('最优解为：', bv, '取得最优解时自变量为', bs)

第6题

最优解为： -2 取得最优解时自变量为 [-2, 2, 2]

# 下山法
import random

# 给出x1,x2,x3取值范围
xr = [[-2, 5], [2, 6], [-5, 2]]

# 随机选择初始值，确保在范围内
bs = [random.randint(r[0], r[1]) for r in xr]

def f(x1, x2, x3):
    y = x1 + x2 - x3
    return y

# bev：bestevaluete, bv:bestvalue
while True:
    bev = f(bs[0], bs[1], bs[2])
    bv = bev
    so = [bs]
    t = len(bs)
    for i in range(t):
        if bs[i] > xr[i][0]:
            so.append(bs[0:i] + [bs[i]-1] + bs[i+1:])
        if bs[i] < xr[i][1]:
            so.append(bs[0:i] + [bs[i]+1] + bs[i+1:])
    for s in so:
        el = f(s[0], s[1], s[2])
        # 取所有el中最小的
        if el < bev:
            bs = s
            bev = el
    print(bs, bev)
    if bev == bv:
        break

print('最优解为：', bv, '取得最优解时自变量为', bs)

第8题

最优点: (0.0000, 0.0000)
函数最小值: 0.0000

import math

# 目标函数
def f(x, y):
    return x**2 + y**2

# 梯度函数
def grad(x, y):
    return (2 * x , 2 * y)

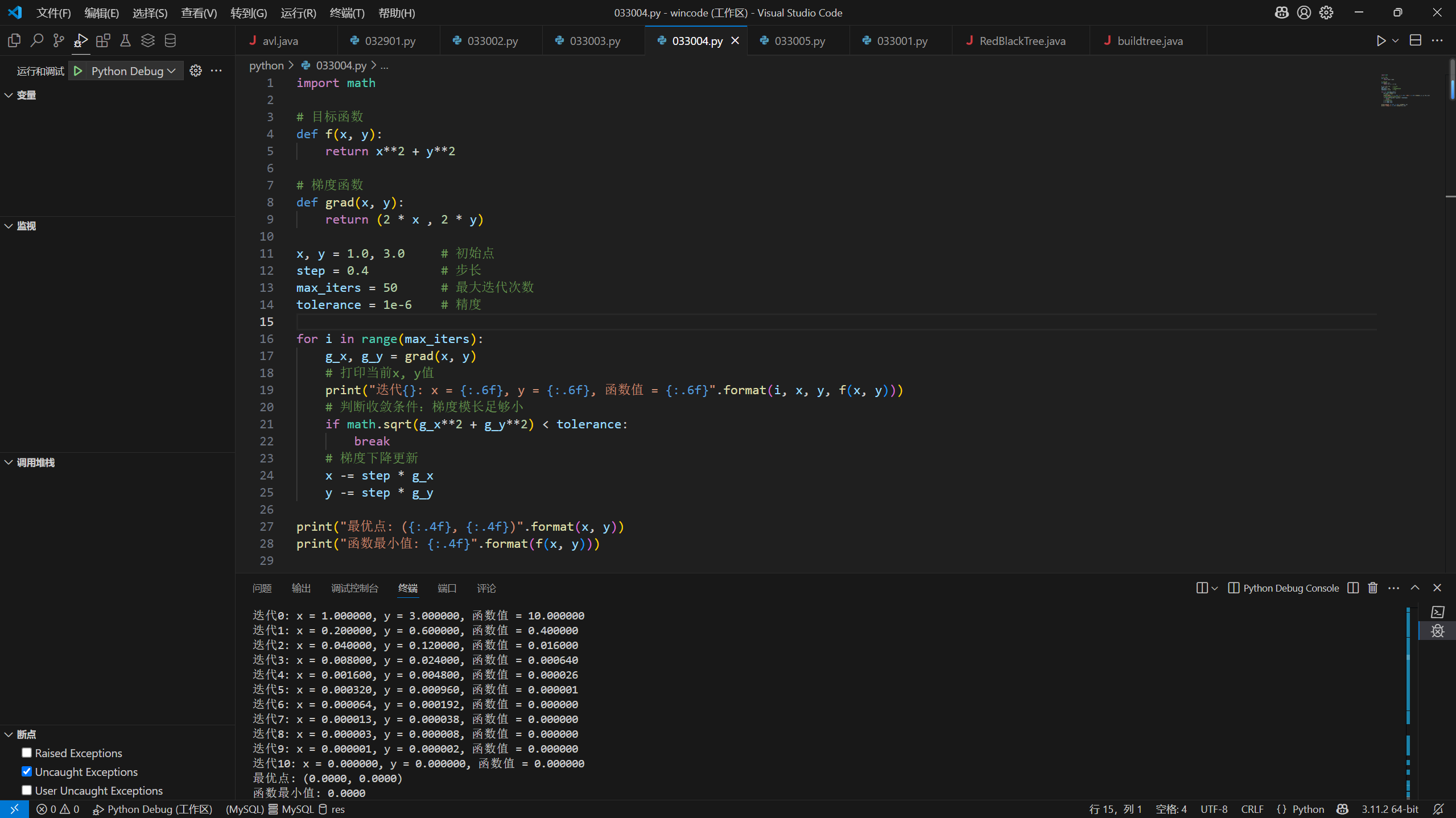
x, y = 1.0, 3.0     # 初始点
step = 0.4          # 步长
max_iters = 50      # 最大迭代次数
tolerance = 1e-6    # 精度

for i in range(max_iters):
    g_x, g_y = grad(x, y)
    # 打印当前x, y值
    print("迭代{}: x = {:.6f}, y = {:.6f}, 函数值 = {:.6f}".format(i, x, y, f(x, y)))
    # 判断收敛条件：梯度模长足够小
    if math.sqrt(g_x**2 + g_y**2) < tolerance:
        break
    # 梯度下降更新
    x -= step * g_x
    y -= step * g_y

print("最优点: ({:.4f}, {:.4f})".format(x, y))
print("函数最小值: {:.4f}".format(f(x, y)))

第10题

近似根: (0.999530, 0.000000)
函数值: 0.000000

import math

# 目标函数
def f(x, y):
    return 2 * (x - 1)**2 + y**2

# 梯度函数
def grad(x, y):
    return (4 * (x - 1), 2 * y)

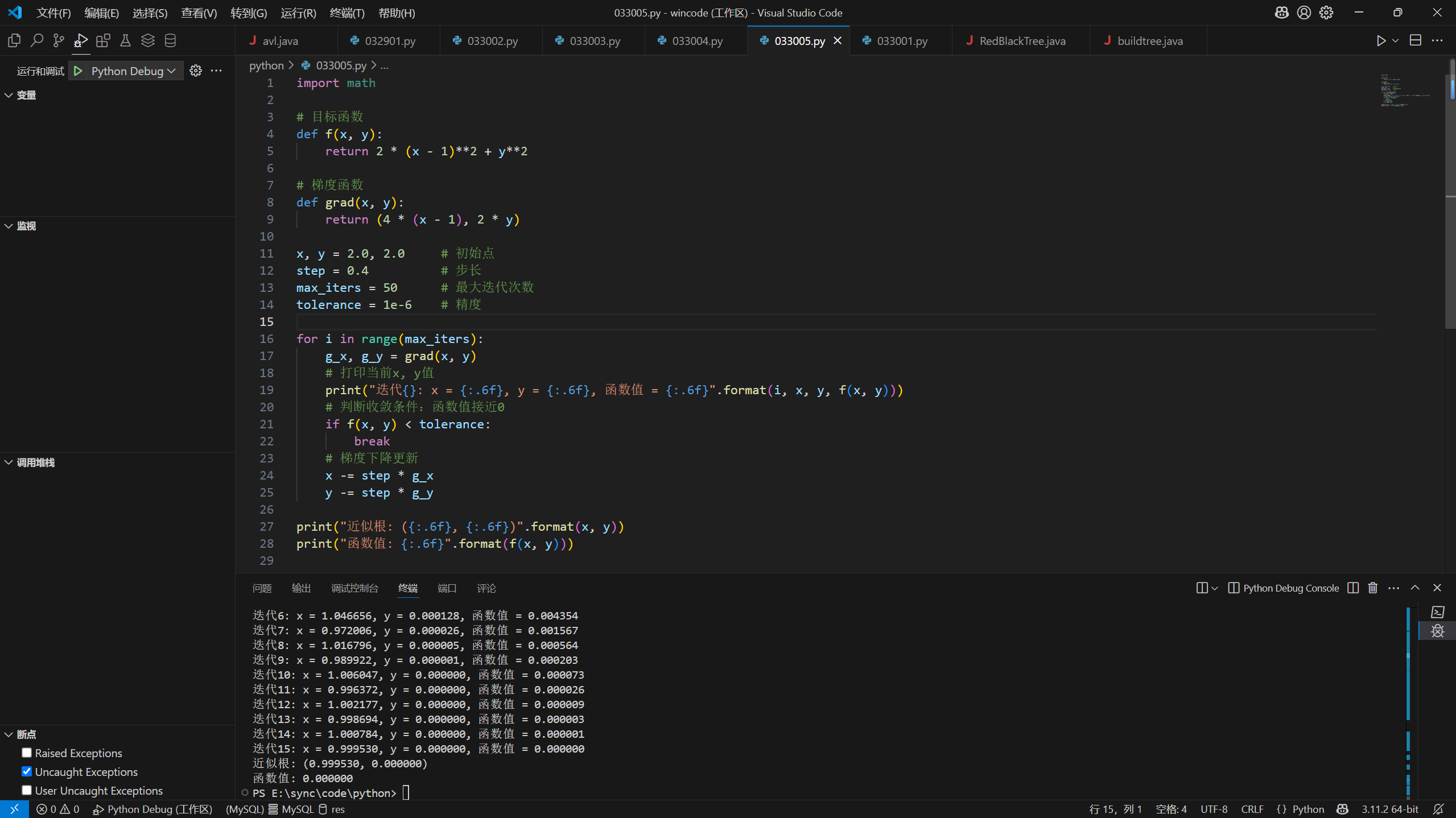
x, y = 2.0, 2.0     # 初始点
step = 0.4          # 步长
max_iters = 50      # 最大迭代次数
tolerance = 1e-6    # 精度

for i in range(max_iters):
    g_x, g_y = grad(x, y)
    # 打印当前x, y值
    print("迭代{}: x = {:.6f}, y = {:.6f}, 函数值 = {:.6f}".format(i, x, y, f(x, y)))
    # 判断收敛条件：函数值接近0
    if f(x, y) < tolerance:
        break
    # 梯度下降更新
    x -= step * g_x
    y -= step * g_y

print("近似根: ({:.6f}, {:.6f})".format(x, y))
print("函数值: {:.6f}".format(f(x, y)))

习题2.1

第2题

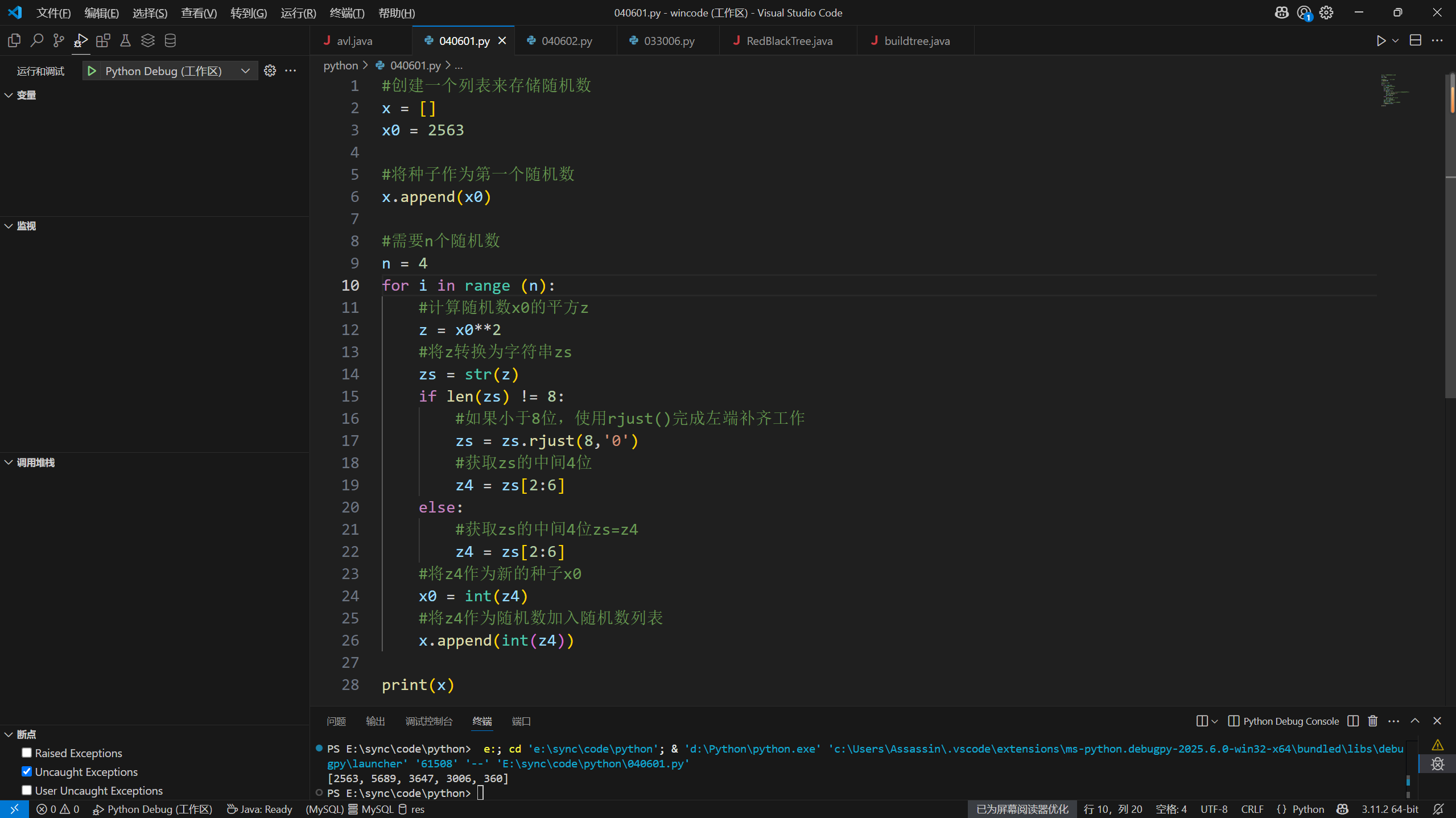
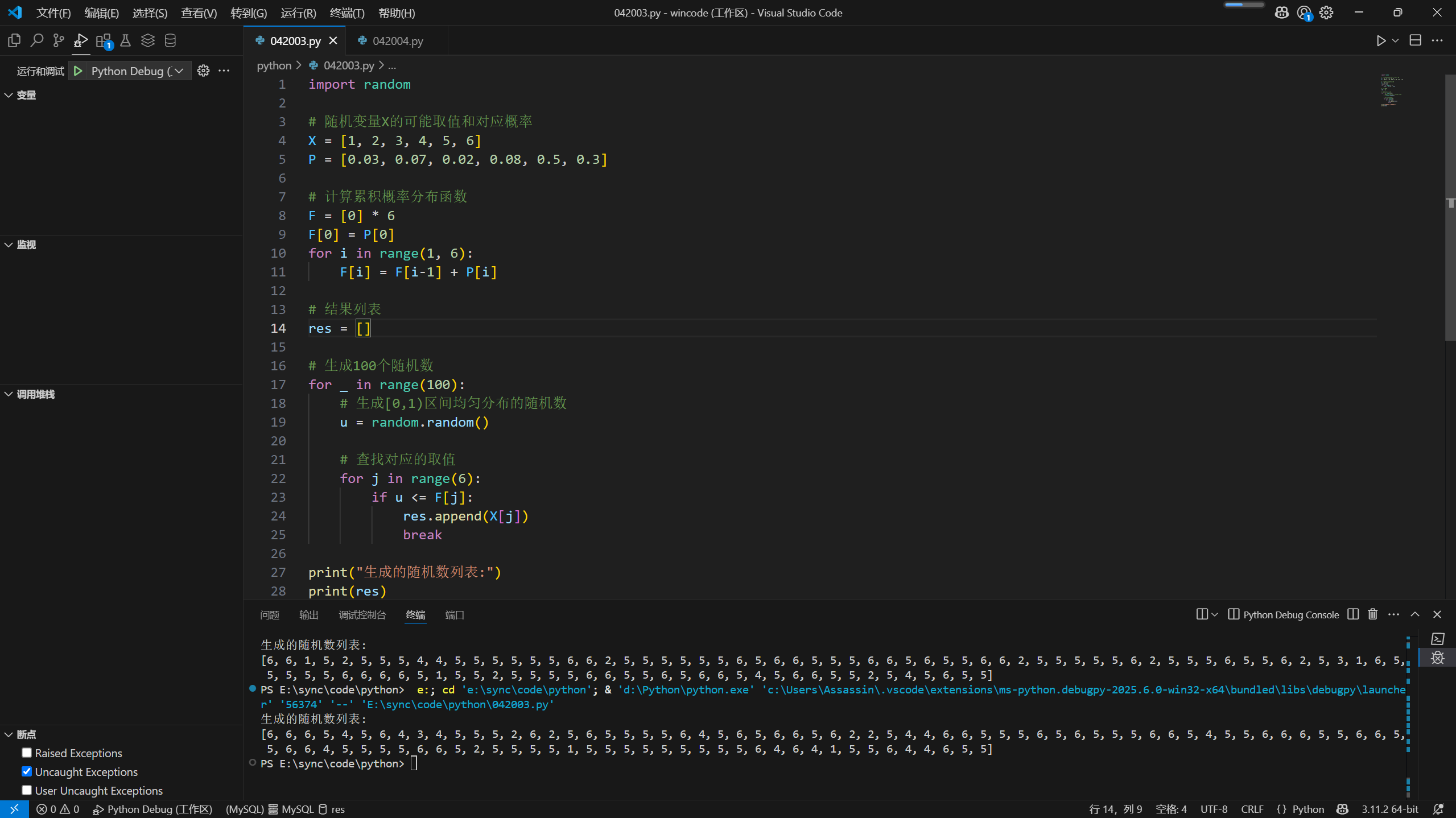
4个随机数为：[2563, 5689, 3647, 3006, 360]

#创建一个列表来存储随机数
x = [] 
x0 = 2563

#将种子作为第一个随机数
x.append(x0) 

#需要n个随机数
n = 4
for i in range (n):
    #计算随机数x0的平方z
    z = x0**2 
    #将z转换为字符串zs
    zs = str(z)
    if len(zs) != 8:
        #如果小于8位，使用rjust()完成左端补齐工作
        zs = zs.rjust(8,'0') 
        #获取zs的中间4位
        z4 = zs[2:6] 
    else:
        #获取zs的中间4位zs=z4
        z4 = zs[2:6] 
    #将z4作为新的种子x0
    x0 = int(z4)  
    #将z4作为随机数加入随机数列表
    x.append(int(z4)) 

print(x)

第3题

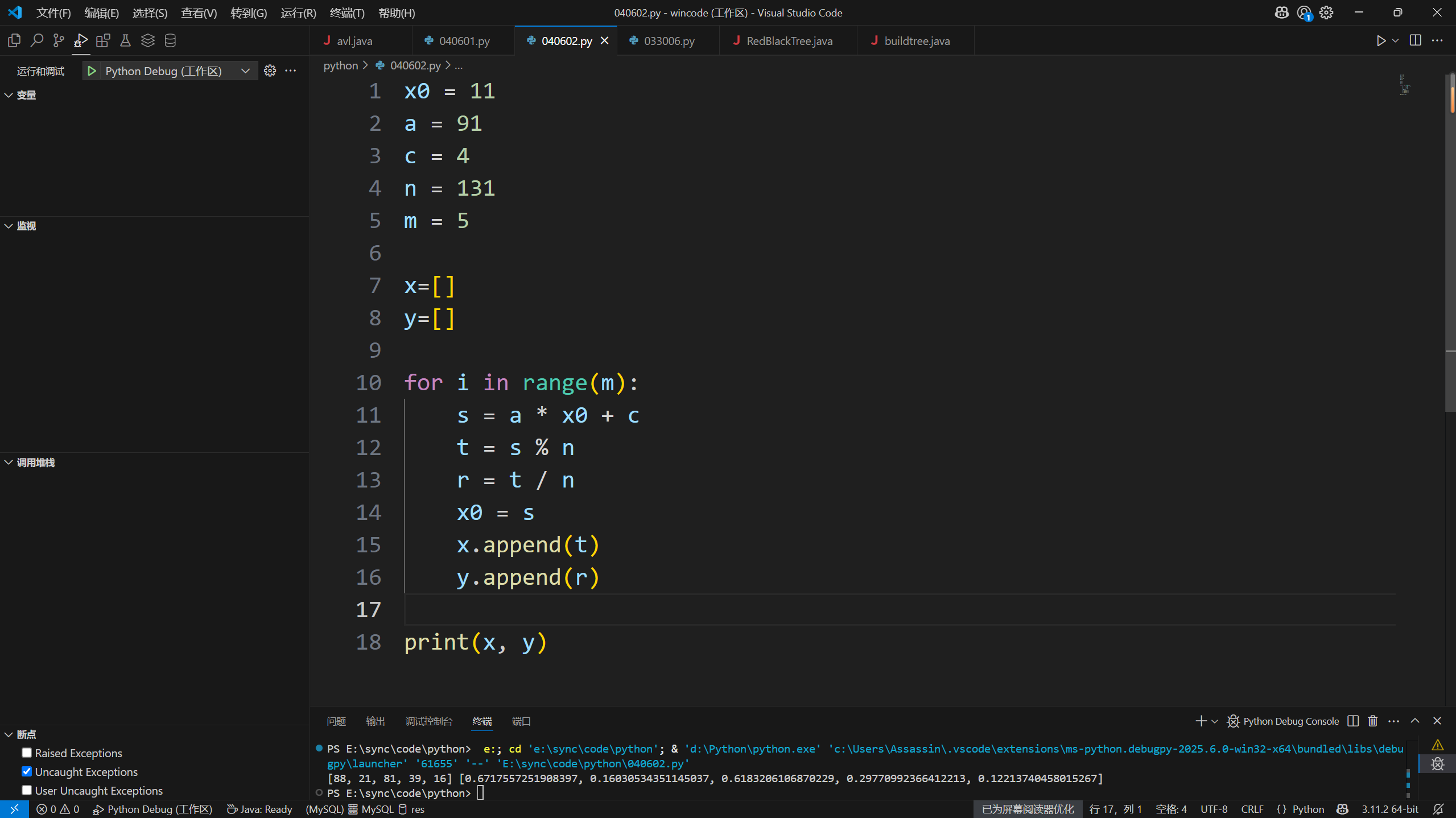
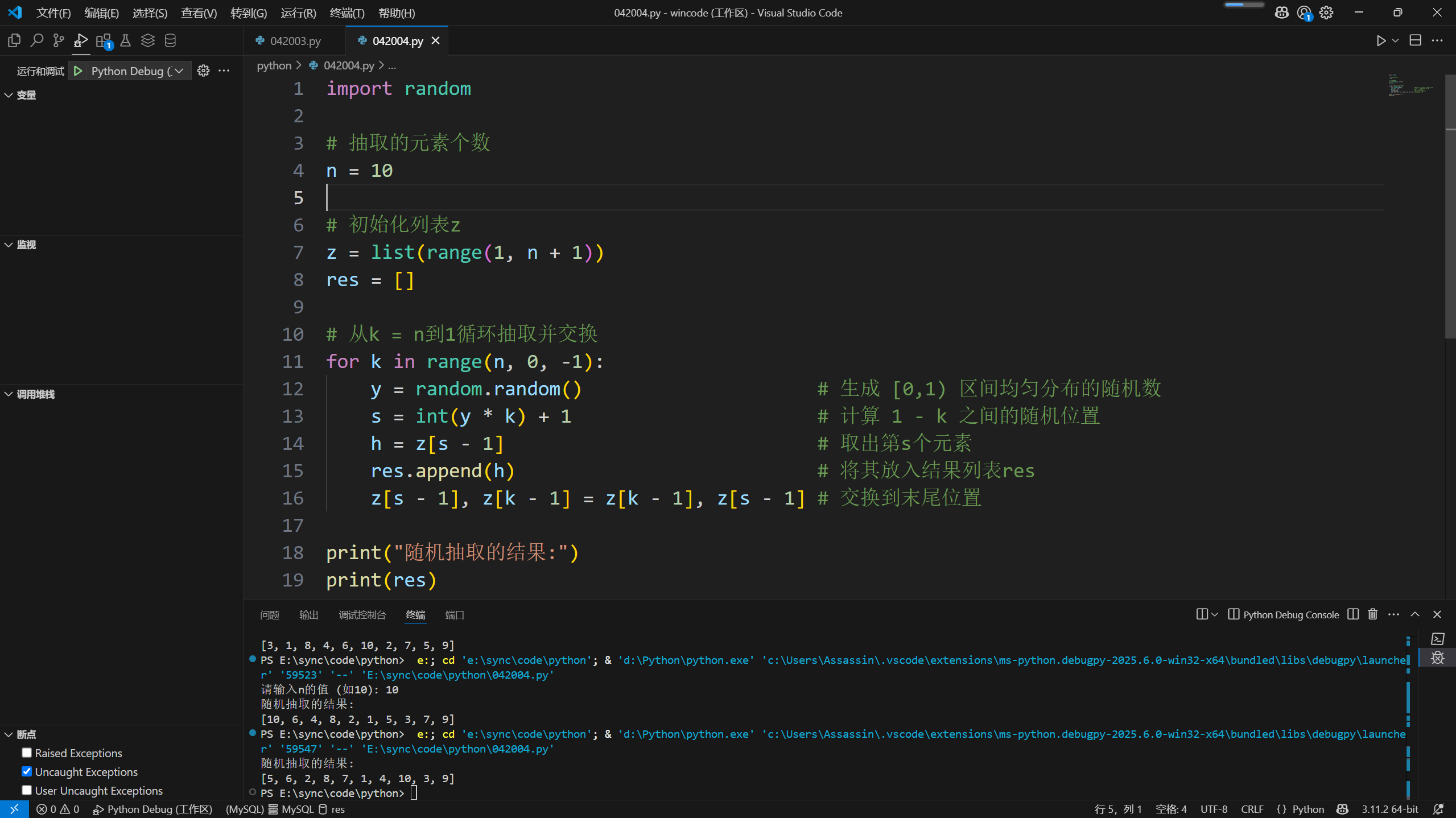
5个随机数：[0.6717557251908397, 0.16030534351145037, 0.6183206106870229, 0.29770992366412213, 0.12213740458015267]

x0 = 11
a = 91
c = 4
n = 131
m = 5

x=[]
y=[]

for i in range(m):
    s = a * x0 + c
    t = s % n
    r = t / n
    x0 = s
    x.append(t)
    y.append(r)

print(x, y)

习题2.3

第1题

$$F[x]=\left\{\begin{array}{cc}0, & x<1 \\ 0.03, & 1<x \leq 2 \\ 0.1, & 2<x \leq 3 \\ 0.12, & 3<x \leq 4 \\ 0.2, & 4<x \leq 5 \\ 0.7, & 5<x \leq 6 \\ 1, & x \geq 6\end{array}\right.$$

import random

# 随机变量X的可能取值和对应概率
X = [1, 2, 3, 4, 5, 6]
P = [0.03, 0.07, 0.02, 0.08, 0.5, 0.3]

# 计算累积概率分布函数
F = [0] * 6
F[0] = P[0]
for i in range(1, 6):
    F[i] = F[i-1] + P[i]

# 结果列表
res = []

# 生成100个随机数
for _ in range(100):
    # 生成[0,1)区间均匀分布的随机数
    u = random.random()
    
    # 查找对应的取值
    for j in range(6):
        if u <= F[j]:
            res.append(X[j])
            break

print("生成的随机数列表:")
print(res)

第2题

$s=\lfloor y \cdot k\rfloor+1$

import random

# 抽取的元素个数
n = 10

# 初始化列表z
z = list(range(1, n + 1))
res = []

# 从k = n到1循环抽取并交换
for k in range(n, 0, -1):
    y = random.random()                     # 生成 [0,1) 区间均匀分布的随机数
    s = int(y * k) + 1                      # 计算 1 - k 之间的随机位置
    h = z[s - 1]                            # 取出第s个元素
    res.append(h)                           # 将其放入结果列表res
    z[s - 1], z[k - 1] = z[k - 1], z[s - 1] # 交换到末尾位置

print("随机抽取的结果:")
print(res)

习题2.5

第4题

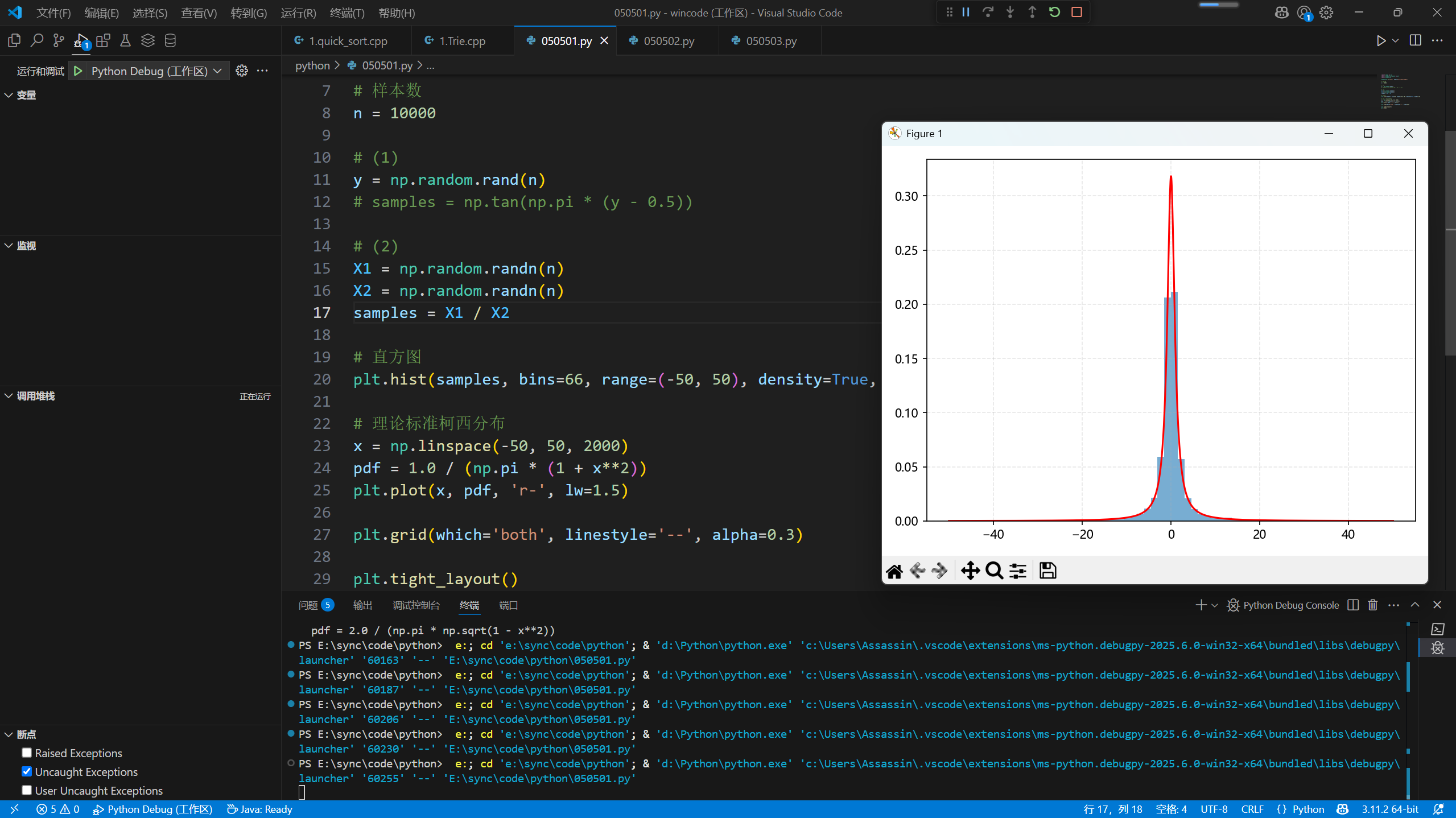
(1) 逆变换法
分布函数

$$F(x)=\frac1\pi\arctan x + \frac12.$$

逆变换

$$y=F(x)\quad\Longrightarrow\quad x = \tan\bigl[\pi\,(y-\tfrac12)\bigr].$$

(2)
利用定理：若 $X_1,X_2\sim N(0,1)$ 且独立，则

$$\frac{X_1}{X_2}\sim\mathrm{Cauchy}(0,1).$$

import numpy as np
import matplotlib.pyplot as plt
import matplotlib

matplotlib.rc("font", family='MicroSoft YaHei')

# 样本数
n = 10000

# (1)
y = np.random.rand(n)
# samples = np.tan(np.pi * (y - 0.5))

# (2)
X1 = np.random.randn(n)
X2 = np.random.randn(n)
samples = X1 / X2

# 直方图
plt.hist(samples, bins=66, range=(-50, 50), density=True, alpha=0.6)

# 理论标准柯西分布
x = np.linspace(-50, 50, 2000)
pdf = 1.0 / (np.pi * (1 + x**2))
plt.plot(x, pdf, 'r-', lw=1.5)

plt.grid(which='both', linestyle='--', alpha=0.3)

plt.tight_layout()
plt.show()

第8题

$$F(x) = \int_{0}^{x}\frac{2}{\pi\sqrt{1-t^2}}\,dt = \frac{2}{\pi}\arcsin(x)\,,\quad 0 \le x < 1.$$

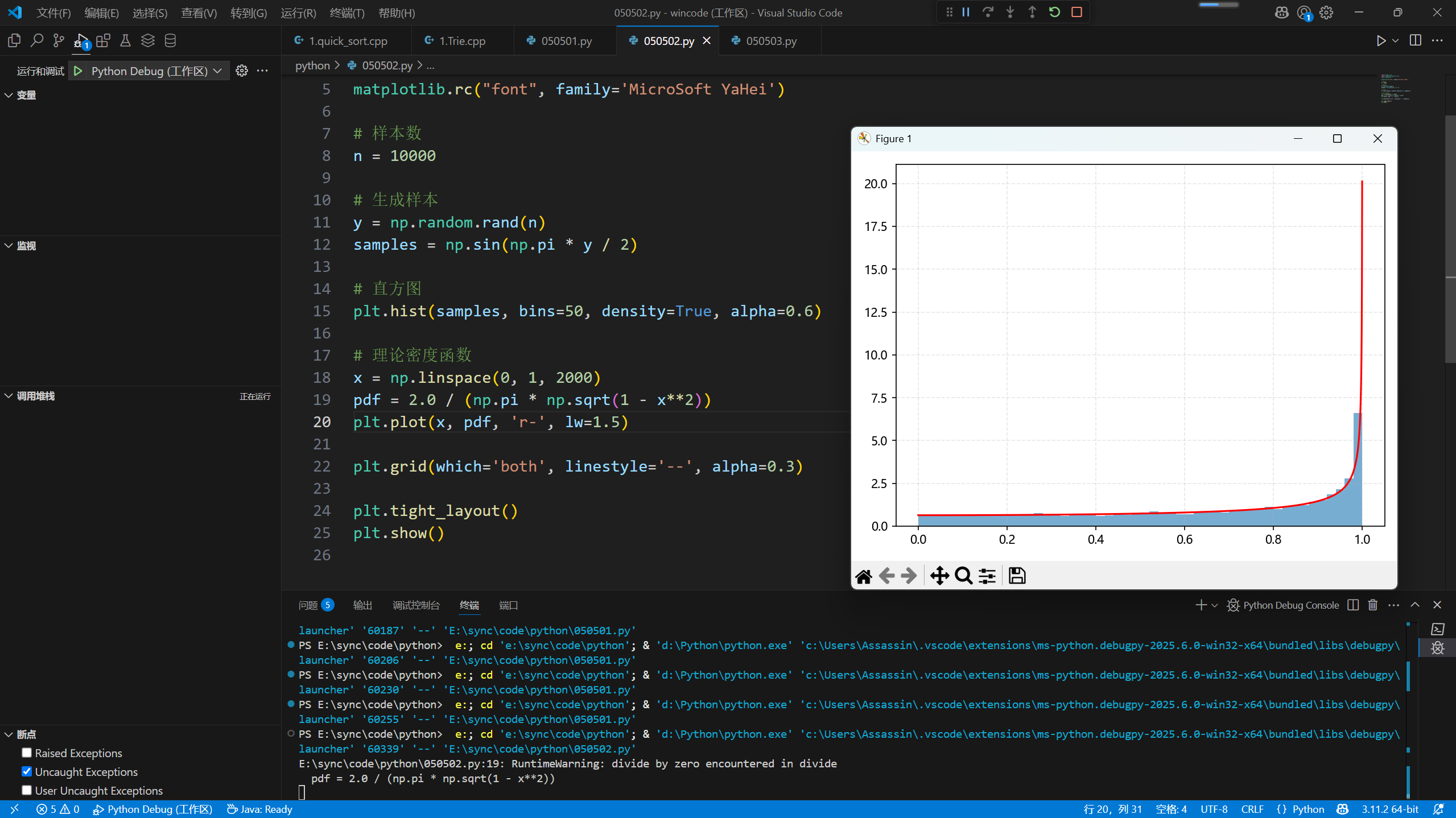
令 $Y\sim \mathrm{Unif}(0,1)$

$$Y = F(X) = \frac{2}{\pi}\arcsin(X) \;\Longrightarrow\; \arcsin(X) = \frac{\pi}{2}Y \;\Longrightarrow\; X = \sin\!\Bigl(\tfrac{\pi}{2}Y\Bigr).$$

import numpy as np
import matplotlib.pyplot as plt
import matplotlib

matplotlib.rc("font", family='MicroSoft YaHei')

# 样本数
n = 10000

# 生成样本
y = np.random.rand(n)
samples = np.sin(np.pi * y / 2)

# 直方图
plt.hist(samples, bins=50, density=True, alpha=0.6)

# 理论密度函数
x = np.linspace(0, 1, 2000)
pdf = 2.0 / (np.pi * np.sqrt(1 - x**2))
plt.plot(x, pdf, 'r-', lw=1.5)

plt.grid(which='both', linestyle='--', alpha=0.3)

plt.tight_layout()
plt.show()

第13题

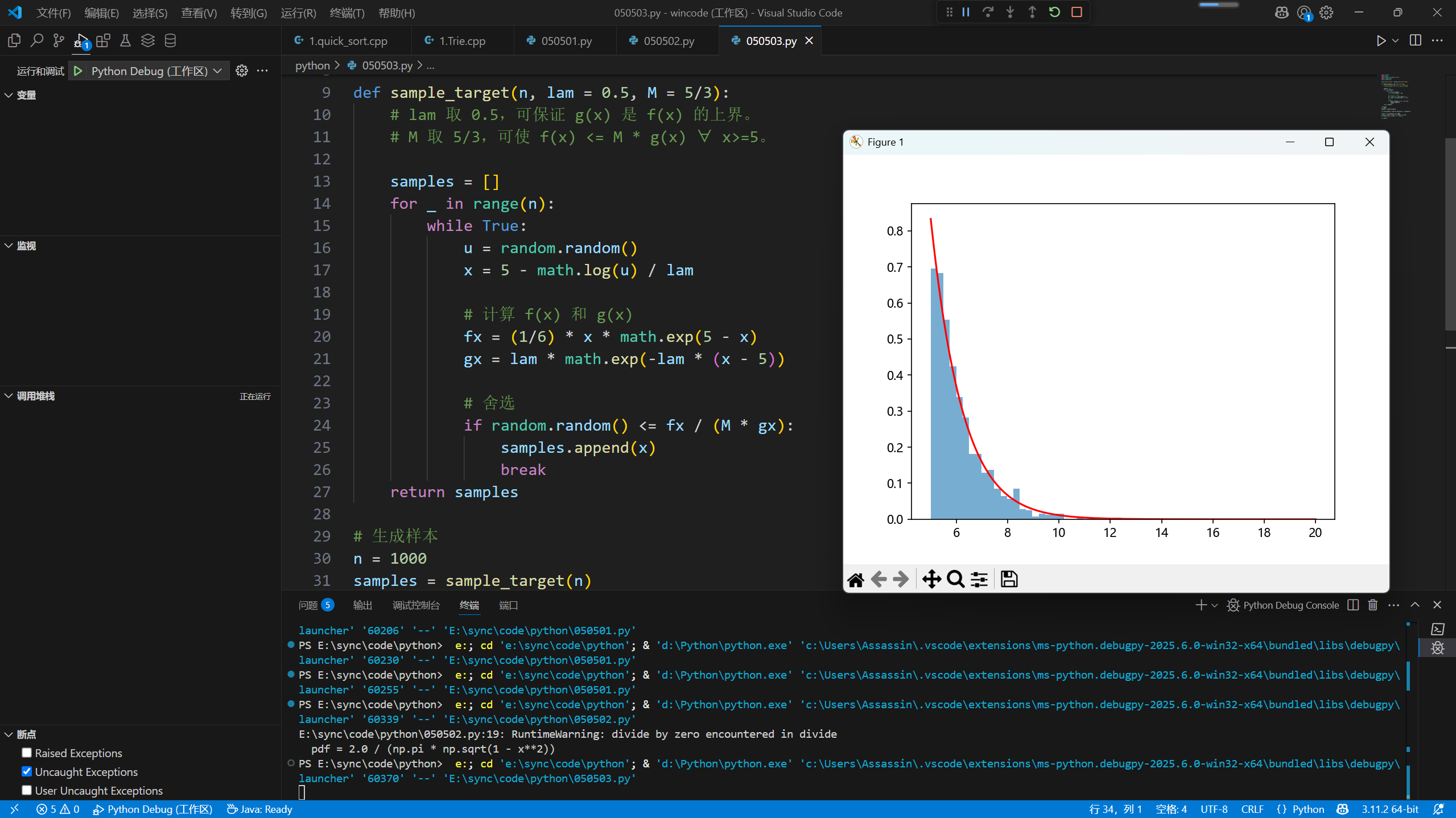
生成一个从 5 开始、参数为 $\lambda$ 的“平移后”指数分布样本。
标准指数分布：

$$F_{\text{std}}(t) = 1 - e^{-\lambda t}, \quad t \geq 0.$$

生成 $u \sim \text{Uniform}(0,1)$。
解 $u = F_{\text{std}}(t) = 1 - e^{-\lambda t}$，得到：

$$t = -\frac{1}{\lambda} \ln(1 - u).$$

$1 - u$ 与 $u$ 在分布上是等价的（Uniform(0,1)），可以简化为：

$$t = -\frac{1}{\lambda} \ln(u).$$

平移回 $x = t + 5$，得到：

$$x = 5 - \frac{1}{\lambda} \ln(u).$$

从 5 开始的指数分布，在任意 $x \geq 5$ 上的概率密度函数是：

$$g(x) = \lambda \, e^{-\lambda (x - 5)}, \quad x \geq 5.$$

import random
import math
import matplotlib.pyplot as plt
import numpy as np
import matplotlib

matplotlib.rc("font", family='MicroSoft YaHei')

def sample_target(n, lam = 0.5, M = 5/3):
    # lam 取 0.5，可保证 g(x) 是 f(x) 的上界。
    # M 取 5/3，可使 f(x) <= M * g(x) ∀ x>=5。

    samples = []
    for _ in range(n):
        while True:
            u = random.random()
            x = 5 - math.log(u) / lam

            # 计算 f(x) 和 g(x)
            fx = (1/6) * x * math.exp(5 - x)
            gx = lam * math.exp(-lam * (x - 5))

            # 舍选
            if random.random() <= fx / (M * gx):
                samples.append(x)
                break
    return samples

# 生成样本
n = 1000
samples = sample_target(n)

plt.hist(samples, bins=30, density=True, alpha=0.6)

x_vals = np.linspace(5, 20, 1000)
y_vals = (1/6) * x_vals * np.exp(5 - x_vals)
plt.plot(x_vals, y_vals, 'r-', lw=1.5)

plt.show()

习题3.1

第5题

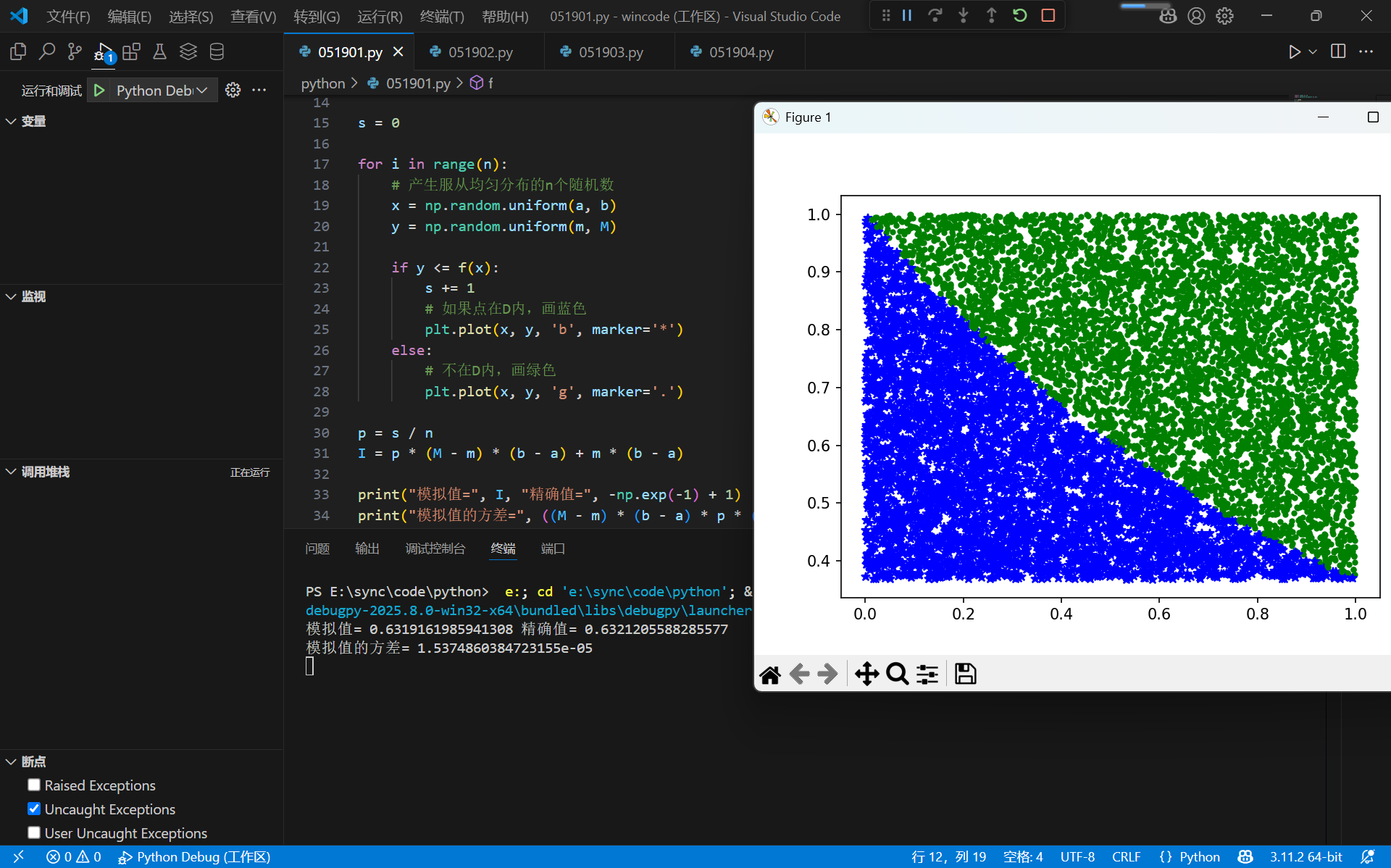
1. 随机投点法

   $\hat{I}_1=(b-a)(d-c)p + c(b - a)$

   $D\left(\hat{I}_1\right)=\frac{(b-a)(d-c) p(1-p)}{N}$

   import numpy as np
   import matplotlib.pyplot as plt
   
   n = 10000
   a = 0
   b = 1
   m = np.exp(-1)
   M = 1
   
   # 定义函数f(x)
   def f(x):
       t = np.exp(-x)
       return t
   
   s = 0
   
   for i in range(n):    
       # 产生服从均匀分布的n个随机数
       x = np.random.uniform(a, b) 
       y = np.random.uniform(m, M) 
   
       if y <= f(x):
           s += 1
           # 如果点在D内，画蓝色
           plt.plot(x, y, 'b', marker='*') 
       else:
           # 不在D内，画绿色
           plt.plot(x, y, 'g', marker='.') 
   
   p = s / n
   I = p * (M - m) * (b - a) + m * (b - a)
   
   print("模拟值=", I, "精确值=", -np.exp(-1) + 1)
   print("模拟值的方差=", ((M - m) * (b - a) * p * (1 - p)) / n)
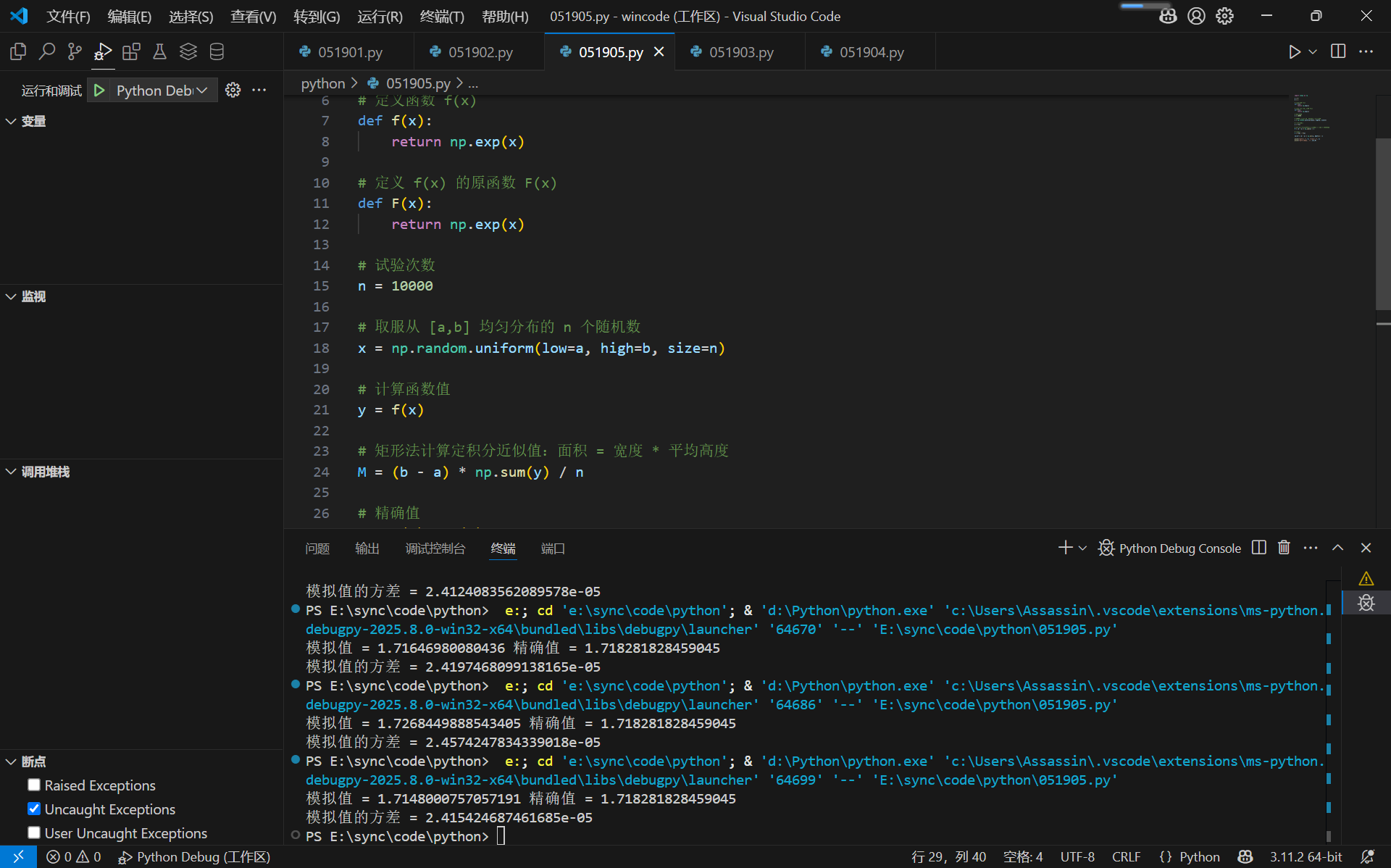
   plt.show()

   

2. 平均值法

   $$\hat{I}_2=\frac{b-a}{n} \sum_{i=1}^n f\left(x_i\right)$$ $$D\left(\hat{I}_2\right)=\frac{b-a}{n} D(f(x))$$

   import numpy as np
   
   a = 0
   b = 1
   
   # 定义函数 f(x)
   def f(x):
       return np.exp(-x)
   
   # 定义 f(x) 的原函数 F(x)
   def F(x): 
       return -np.exp(-x)
   
   # 试验次数
   n = 10000
   
   # 取服从 [a,b] 均匀分布的 n 个随机数
   x = np.random.uniform(low=a, high=b, size=n) 
   
   # 计算函数值
   y = f(x)
   
   # 矩形法计算定积分近似值：面积 = 宽度 * 平均高度
   M = (b - a) * np.sum(y) / n 
   
   # 精确值
   I = F(b) - F(a) 
   
   var_M = (b - a) * np.var(y, ddof=1) / n
   
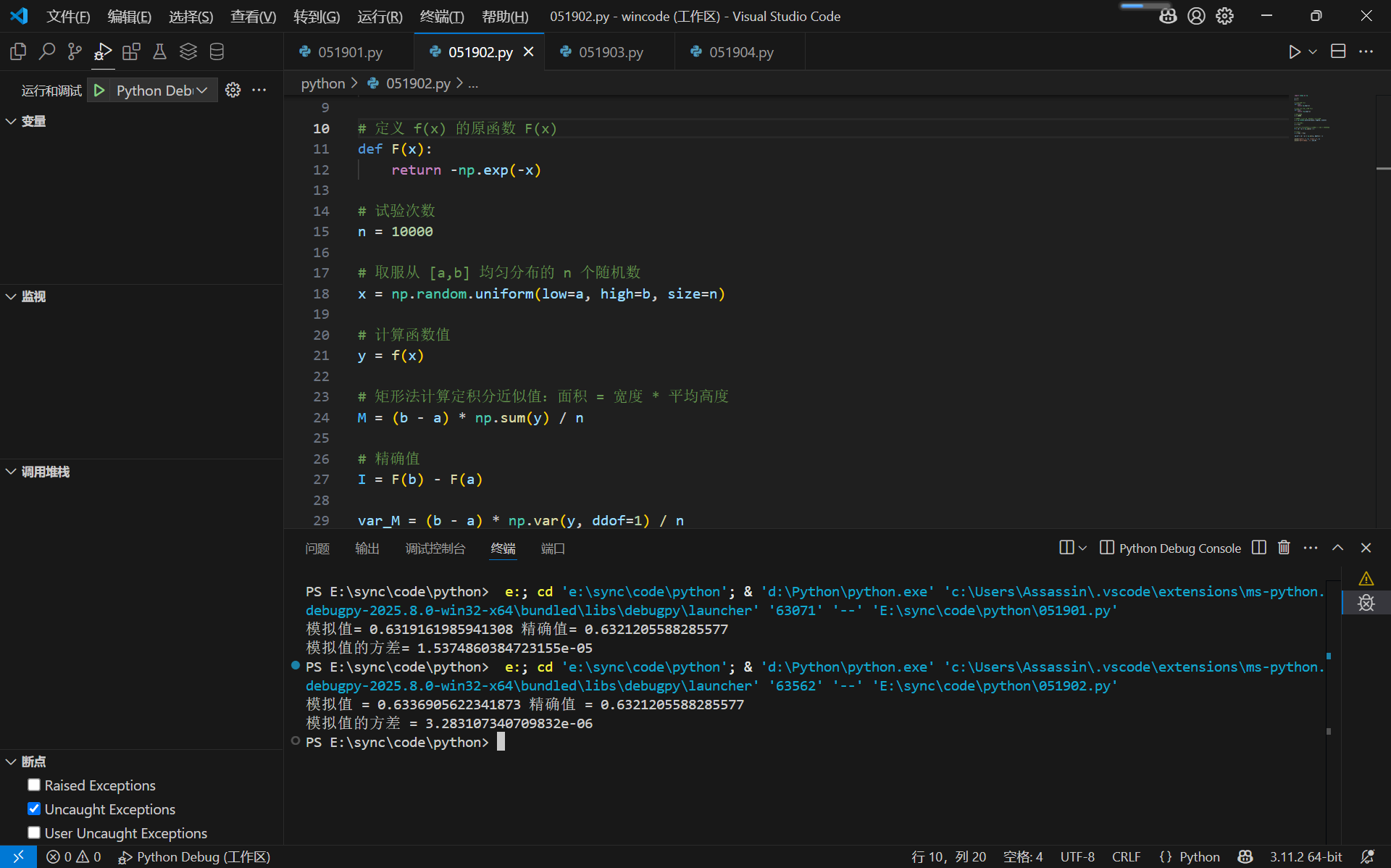
   print("模拟值 =", M, "精确值 =", I)
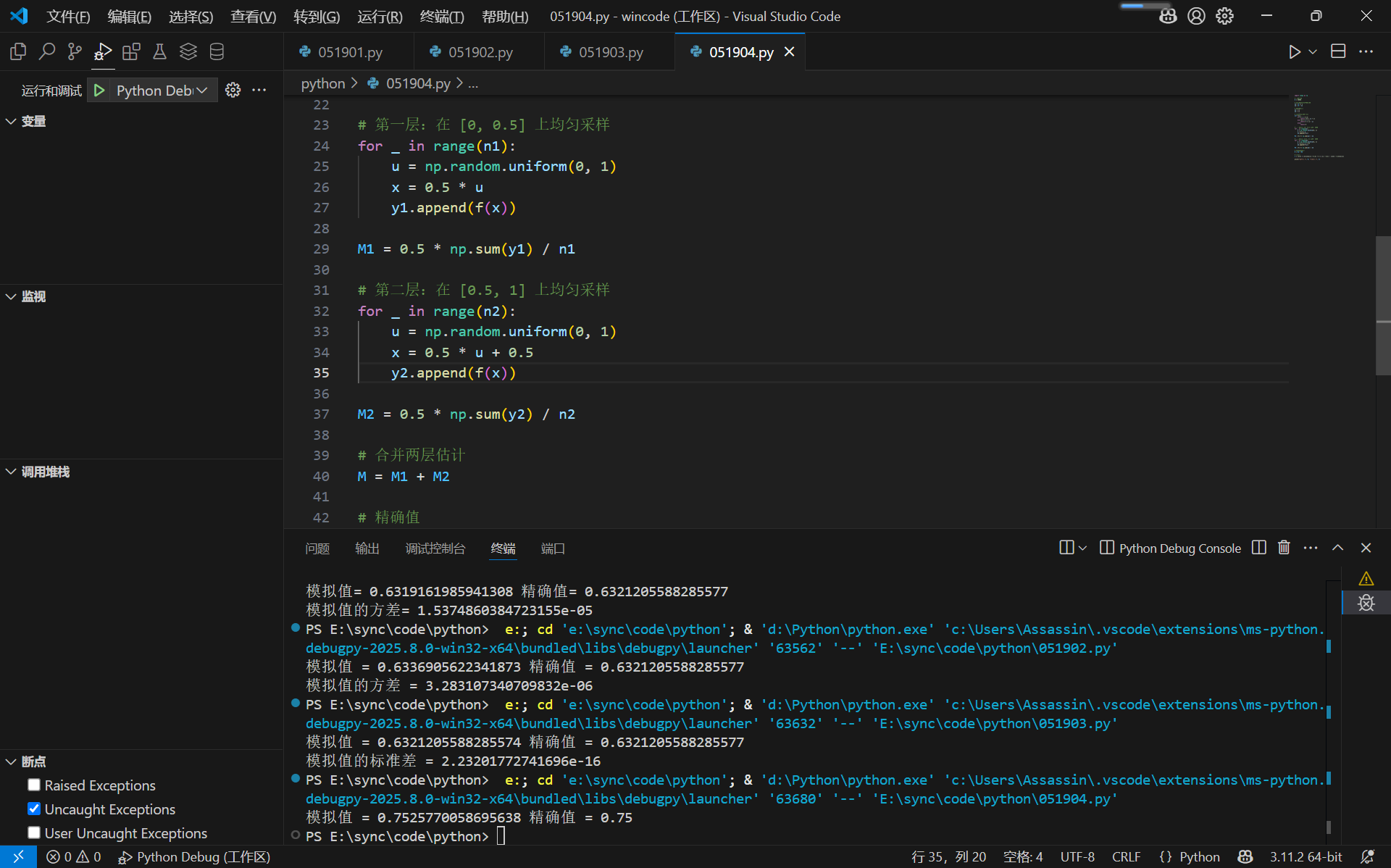
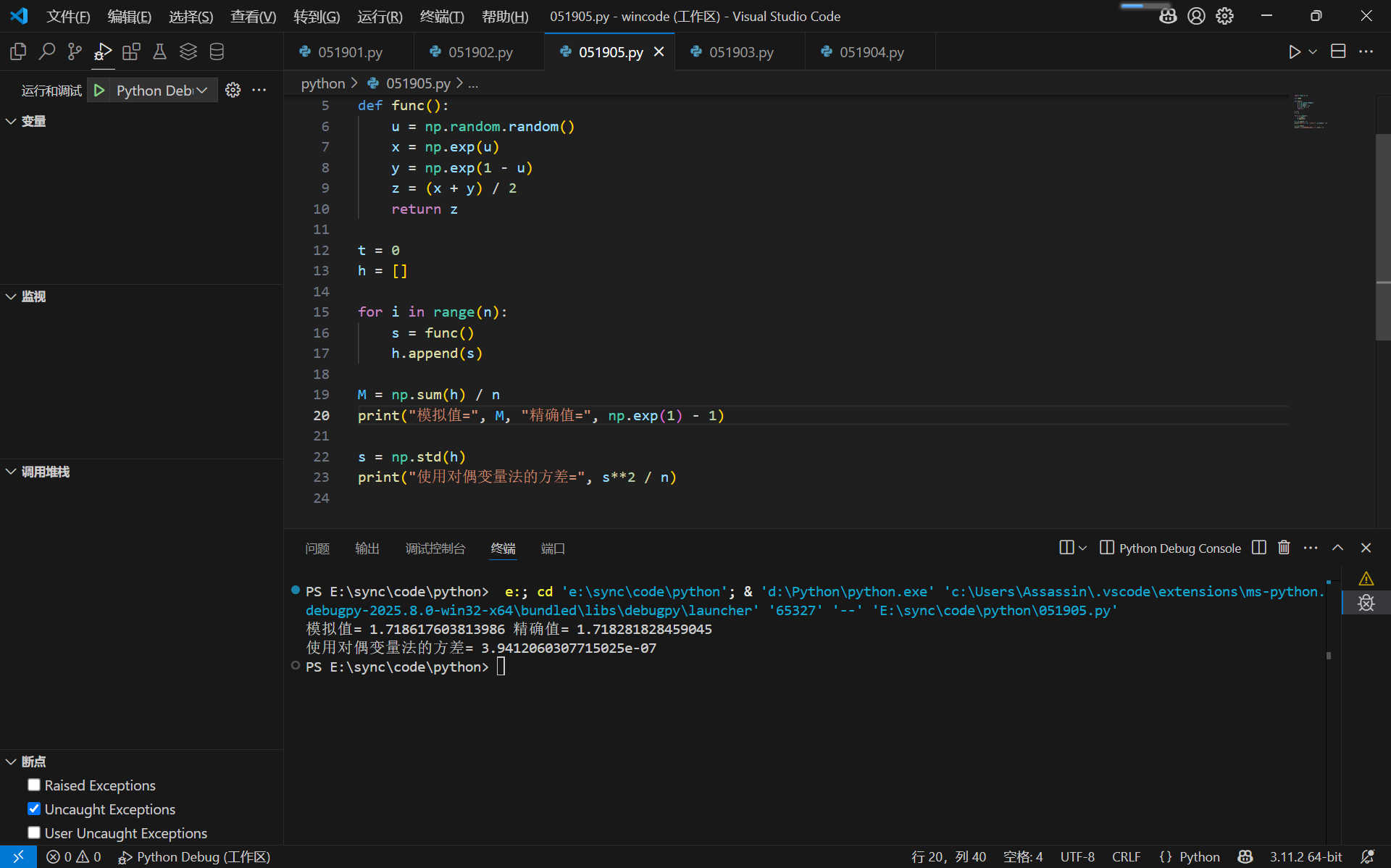
   print("模拟值的方差 =", var_M)

   

3. 重要抽样法

   import numpy as np
   
   n = 10000
   h = []
   a = 0
   b = 1
   
   # 定义 f(x) 的原函数 F(x)
   def F(x): 
       return -np.exp(-x)
   
   for i in range(n):
       # 取服从[0,1]均匀分布的随机数
       u = np.random.random()
       
       # 反函数法从 g(x) 中抽样
       x = -np.log(1 - (1 - np.exp(-1)) * u)
       
       # 目标函数 f(x)
       f = np.exp(-x)
       
       # 拟合函数 g(x)
       g = np.exp(-x) / (1 - np.exp(-1))
       
       # 计算 f/g 比值
       y = f / g
       
       h.append(y)
   
   # 精确值
   I = F(b) - F(a) 
   
   M = np.sum(h) / n
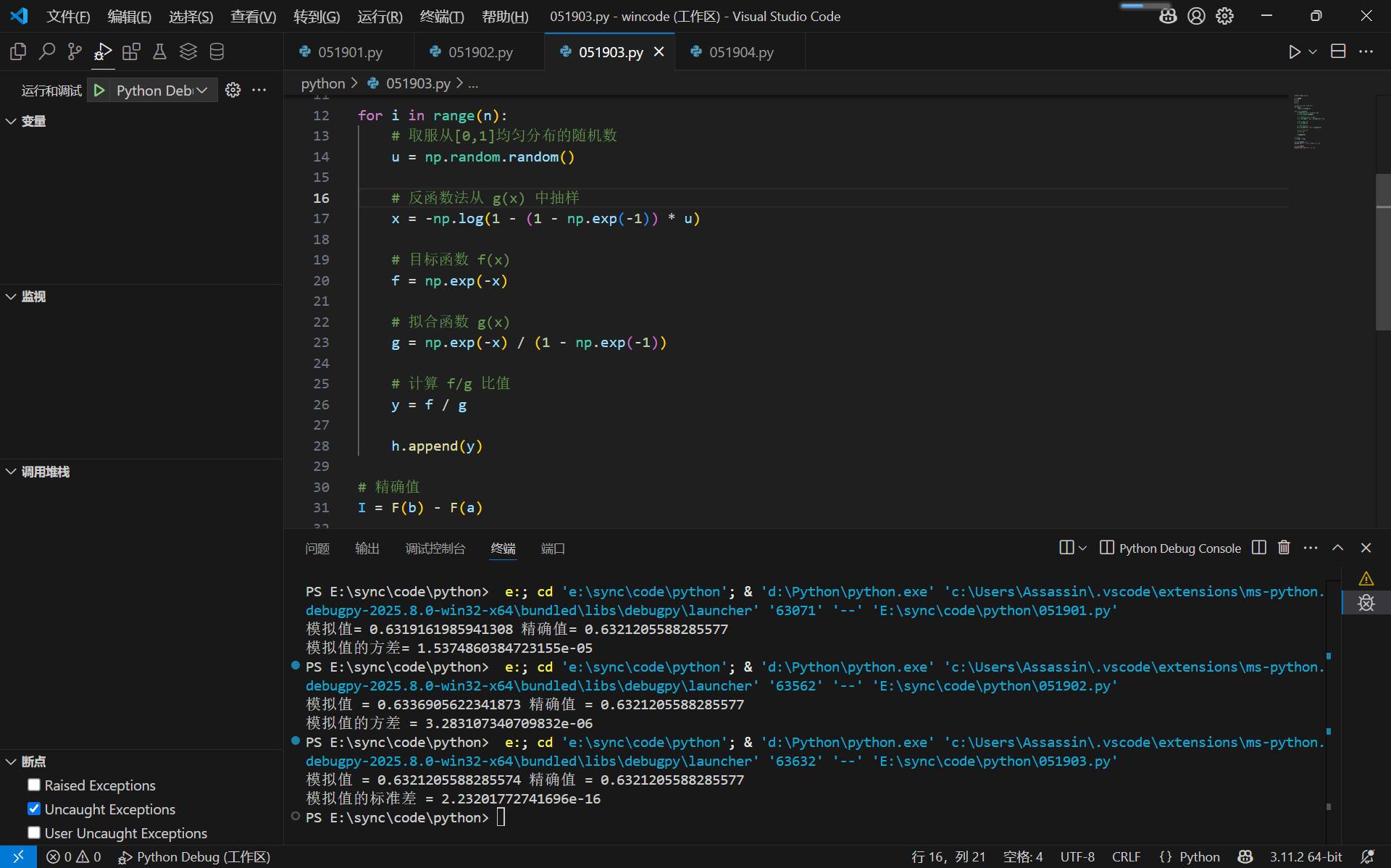
   print("模拟值 =", M, "精确值 =", I)
   
   s = np.std(h)
   print("模拟值的标准差 =", s)

   

第6题

import numpy as np

# 总样本数
N = 50000

# 两个子区间等分样本数
n1 = N // 2
n2 = N - n1

# 存储样本值
y1 = []
y2 = []

# 定义分段函数 f(x)
def f(x):
    if 0 < x < 0.5:
        return 2/5 * (x + 1)
    elif 0.5 < x < 1:
        return 4 * (1 - x)
    else:
        return 0

# 第一层：在 [0, 0.5] 上均匀采样
for _ in range(n1):
    u = np.random.uniform(0, 1)
    x = 0.5 * u
    y1.append(f(x))

M1 = 0.5 * np.sum(y1) / n1

# 第二层：在 [0.5, 1] 上均匀采样
for _ in range(n2):
    u = np.random.uniform(0, 1)
    x = 0.5 * u + 0.5
    y2.append(f(x))

M2 = 0.5 * np.sum(y2) / n2

# 合并两层估计
M = M1 + M2

# 精确值
I = (2/5) * ((0.5**2)/2 + 0.5) + 4 * ((1 - 0.5) - (1**2 - 0.5**2)/2)

print("模拟值 =", M, "精确值 =", I)

习题3.2

第2题

$$\begin{aligned} D(e^{x}) &= E(e^{2x}) - (E(e^{x}))^2 \\ &= \frac{1}{2}(e^{2}-1) - (e-1)^2 \\ &= -\frac{3}{2} + 2e - \frac{1}{2} e^{2} \end{aligned}$$ $$\begin{aligned} D(\hat{I}) &= \frac{1}{n} D(e^{-x}) \\ &= \frac{1}{n}\left( -\frac{3}{2} + 2e - \frac{1}{2} e^{2} \right) \\ &= \frac{0.2405}{n} \end{aligned}$$

import numpy as np

a = 0
b = 1

# 定义函数 f(x)
def f(x):
    return np.exp(x)

# 定义 f(x) 的原函数 F(x)
def F(x): 
    return np.exp(x)

# 试验次数
n = 10000

# 取服从 [a,b] 均匀分布的 n 个随机数
x = np.random.uniform(low=a, high=b, size=n) 

# 计算函数值
y = f(x)

# 矩形法计算定积分近似值：面积 = 宽度 * 平均高度
M = (b - a) * np.sum(y) / n 

# 精确值
I = F(b) - F(a) 

var_M = (b - a) * np.var(y, ddof=1) / n

print("模拟值 =", M, "精确值 =", I)
print("模拟值的方差 =", var_M)

$$\begin{gathered}\hat{\mathrm{I}}_3=\frac{1}{n} \sum_{i=1}^n \frac{e^{U}+e^{1-U}}{2}=\frac{1}{2 n} \sum_{i=1}^n\left(e^{U}+e^{1-U}\right) \\ \mathrm{D}\left(\hat{\mathrm{I}}_3\right)=\frac{1}{4 n}\left(D\left(e^U\right)+D\left(e^{1-U}\right)+2 \operatorname{Cov}\left(e^U, e^{1-U}\right)\right)\end{gathered}$$ $$D\left(e^{U}\right)=E\left(e^{2 U}\right)-\left(E\left(e^{U}\right)\right)^2=\frac{1}{2}\left(e^{2}-1\right)-\left(e-1\right)^2=-\frac{3}{2}+2 e-\frac{1}{2} e^{2}$$ $$\operatorname{Cov}(X, Y)=E(X Y)-E(X) E(Y)=\int_0^1 e^u e^{1-u} d u-\left(\int_0^1 e^u d u\right)^2=e-(e-1)^2$$ $$\mathrm{D}\left(\hat{\mathrm{I}}_3\right)=\frac{1}{4 n}\left(-3 e^2+10 e-5\right)=\frac{0.003913}{n}$$

import numpy as np

n = 10000

def func():
    u = np.random.random()
    x = np.exp(u)
    y = np.exp(1 - u)
    z = (x + y) / 2
    return z

t = 0
h = []

for i in range(n):
    s = func()
    h.append(s)

M = np.sum(h) / n
print("模拟值=", M, "精确值=", np.exp(1) - 1)

s = np.std(h)
print("使用对偶变量法的方差=", s**2 / n)

习题3.3

第1题

1. 一颗骰子掷 4 次至少得到一个 “6”

   $$P_1 = 1 - \left(\frac{5}{6}\right)^4 = 1 - \frac{625}{1296} = \frac{671}{1296} \approx 0.5177$$

2. 两颗骰子掷 24 次至少得到一个 “双六”(6,6)

   $$P_2 = 1 - \left(\frac{35}{36}\right)^{24} \approx 1 - 0.5087 \approx 0.4913$$

$$P_1 \approx 0.5177 > P_2 \approx 0.4913$$

一颗骰子掷 4 次至少出现一次 “6” 的概率更大。

第4题

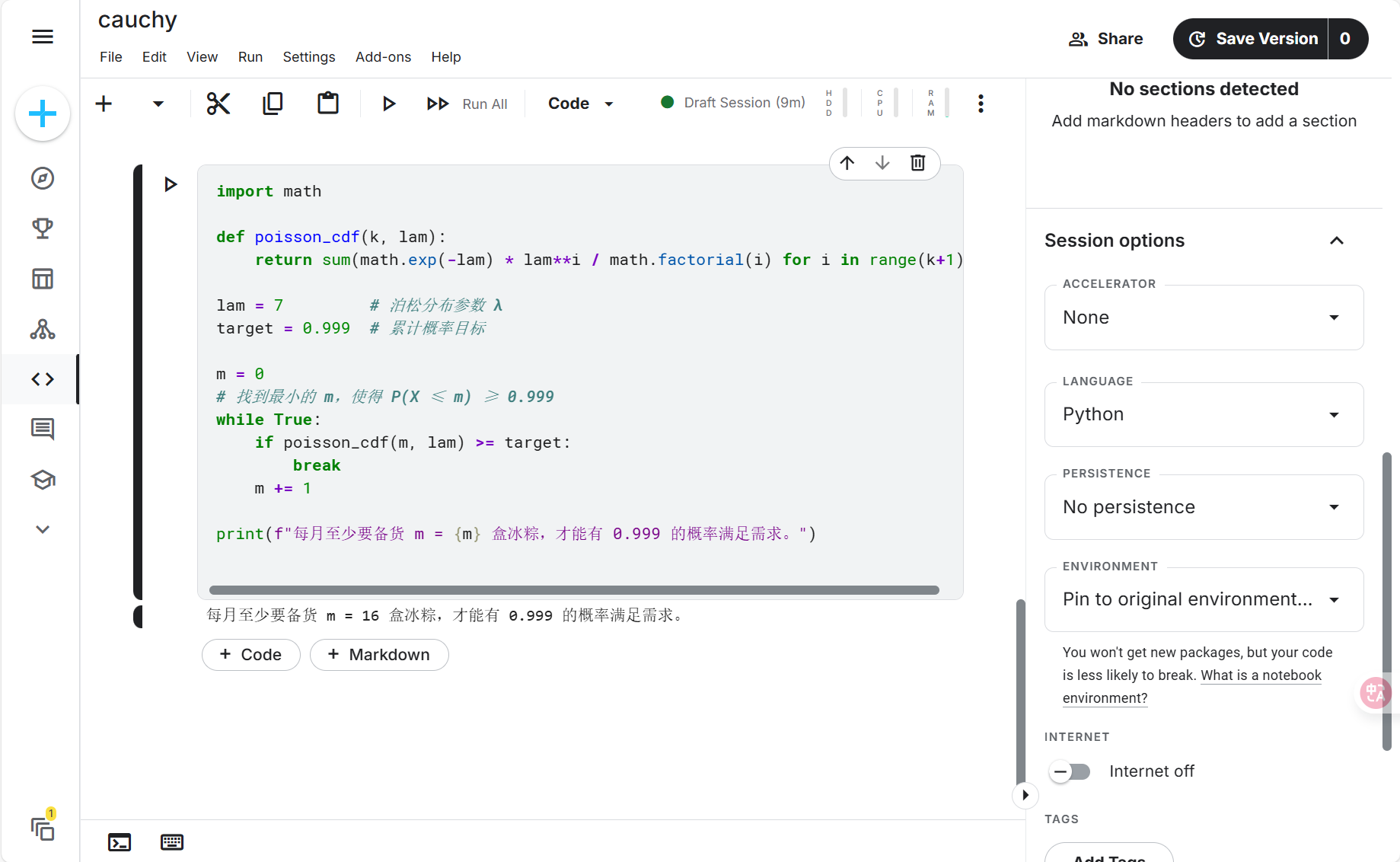
1. 累计分布函数不超过 $m$ 的概率：

   $$P(X \le m) = \sum_{k=0}^{m} \frac{e^{-7} \, 7^k}{k!}$$

2. Python计算最小整数 $m$ ：

   • $P(X \le 15) \approx 0.99759 < 0.999$
   • $P(X \le 16) \approx 0.99904 \ge 0.999$

     import math
     
     def poisson_cdf(k, lam):
         return sum(math.exp(-lam) * lam**i / math.factorial(i) for i in range(k+1))
     
     lam = 7         # 泊松分布参数 λ
     target = 0.999  # 累计概率目标
     
     m = 0
     # 找到最小的 m，使得 P(X ≤ m) ≥ 0.999
     while True:
         if poisson_cdf(m, lam) >= target:
             break
         m += 1
     
     print(f"每月至少要备货 m = {m} 盒冰粽，才能有 0.999 的概率满足需求。")

每月需要至少销售 16 盒冰粽，才能保证有 $99.9\%$ 的概率完成业绩要求。

习题3.4

第5题

import numpy as np
from scipy import integrate

def integrand(z, y, x):
    return z * np.sqrt(x**2 + y**2 + 1)

def y_lower(x):
    if 0 <= x <= 2:
        return -(1 - (x-1)**2)**0.5
    else:
        return 0

def y_upper(x):
    if 0 <= x <= 2:
        return (1 - (x-1)**2)**0.5
    else:
        return 0

# 计算三重积分
result, _ = integrate.tplquad(
    integrand,
    0, 2,
    y_lower, y_upper,
    lambda x, y: 0, lambda x, y: 6
)

print(f"积分结果：{result:.6f}")

第13题

复合梯形公式为

$$I=\int_a^b f(x) \mathrm{d} x=\frac{h}{2} \sum_{i=0}^{n-1}\left[f\left(x_i\right)+f\left(x_{i+1}\right)\right]$$

import numpy as np
from scipy import integrate

def integrand(z, y, x):
    return z * np.sqrt(x**2 + y**2 + 1)

def y_lower(x):
    if 0 <= x <= 2:
        return -(1 - (x-1)**2)**0.5
    else:
        return 0

def y_upper(x):
    if 0 <= x <= 2:
        return (1 - (x-1)**2)**0.5
    else:
        return 0

# 计算三重积分
result, _ = integrate.tplquad(
    integrand,
    0, 2,
    y_lower, y_upper,
    lambda x, y: 0, lambda x, y: 6
)

print(f"积分结果：{result:.6f}")

复合辛普森公式为

$$I=\int_a^b f(x) \mathrm{d} x=\frac{h}{6} \sum_{i=0}^{n-1}\left[f\left(x_i\right)+4 f\left(x_{i+1 / 2}\right)+f\left(x_{i+1}\right)\right]$$

import numpy as np
from scipy.integrate import quad

# 定义积分区间 [a, b] 和小区间的数量 n
a = -np.pi / 2
b = np.pi / 2
n = 100

# 计算小区间的长度 h
X = np.linspace(a, b, n + 1)
h = (b - a) / n

# 定义函数
def f(x):
    return (x**3 + np.sin(x)**2) * np.cos(x)**2

# 复合梯形法计算积分（简化变形）
I7 = (2 * np.sum(f(X[1:-1])) + f(a) + f(b)) * h / 2
print(f"复合梯形法的积分结果: {I7}")

# 使用quad计算精确积分值
I, _ = quad(f, a, b)
print(f"使用quad计算的积分值: {I}")

I8 = 0

# 复合辛普森法计算积分
for i in range(n):
        x_i = a + i * h
        I8 += (f(x_i) + 4 * f(x_i + h / 2) + f(x_i + h)) * h / 6

print(f"复合辛普森法的积分结果: {I8}")

# 计算梯形法和辛普森法的相对误差
print(f"使用梯形法的相对误差: {abs(I7 - I) / I}")
print(f"使用辛普森法的相对误差: {abs(I8 - I) / I}")