2023 ICPC Asia EC 网络预选赛
第一场
L KaChang!
Setting the time limit for algorithm competition questions is a very skillful task. If you set the time limit too tight, many people will scold you for being too demanding on details. On the other hand, if you set the time limit too loosely and allow an algorithm with unexpected time complexity to pass, then many people will scold you too.
When preparing problems, people usually set the time limit to at least twice the running time of the standard program, but sometimes contestants still feel that the time limit is too tight.
Now you have the standard program for a problem and another $n$ programs considered “should pass the problem”. Given the running time of each program, please find the smallest integer $k≥2$, so that when the time limit is set to $k$ times the running time of the standard program, all the provided programs can pass. A program can pass if and only if its running time less or equal to the time limit.
Input
The first line contains two integers $n,T (1≤n,T≤10^5)$, representing the number of provided programs (not include the standard program), and the running time of the standard program.
The second line contains $n$ integers $t_1,t_2,…,t_n (1≤t_i≤10^9)$ , representing the running time of the provided programs.
Output
Output a single integer greater or equal to 2, representing the minimin $k$ which could guarantee that all the provided programs can pass.
Input Sample
1 | 5 1000 |
Output Sample
1 | 3 |
1 | 代码长度限制 16 KB |
参考题解
1 |
|
A Qualifiers Ranking Rules
The following is the current ranking rules for the ICPC Asia EC Online Qualifiers, and there will be two online contests.
- In each contest, only the rank of the top-ranked team from each university will be taken as the score of that university;
- In each contest, participating universities will be ranked according to their scores;
- The two rankings of universities are combined using the merge sorting method. For any two universities that obtain the same ranking in different contests, the university that received this ranking in the first contest will be ranked first.
- Delete duplicate universities and obtain the final ranking of all participating universities (only the highest rankings for each university are retained).
Now assuming that there are n teams in the first contest and m teams in the second contest.
For each contest, given the ranking of each team and the university to which it belongs, please output the final ranking of all participating universities according to the above rules.
You can better understand this process through the sample.
Input
The first line contains two integers $n,m (1≤n,m≤10^4)$ , representing the number of teams participating in the first contest and the second contest.
Then following n lines, the $i$-th line contains a string $s_i (1≤∣s_i∣≤10)$ only consisting of uppercase letters, representing the abbreviation of the university to which the $i$-th ranked team in the first contest belongs.
Then following m lines, the $i$-th line contains a string $t_i (1≤∣t_i∣≤10)$ only consisting of uppercase letters, representing the abbreviation of the university to which the $i$-th ranked team in the second contest belongs.
It’s guaranteed that each university has only one abbreviation.
Output
Output several lines, the $i$-th line contains a string, representing the abbreviation of the $i$-th ranked university in the final ranking.
You should ensure that the abbreviation of any participating universities appears exactly once.
Input Sample
1 | 14 10 |
Output Sample
1 | THU |
Hint
Sample is part of the results in 2022 ICPC Asia EC Online Contest.
In the first contest, the ranking of the universities is:
1 | THU |
In the second contest, the ranking of the universities is:
1 | PKU |
By combining these two rankings according to the rules, the rankings of the universities is:
1 | THU |
By deleting duplicate universities we will get the final ranking.
1 | 代码长度限制 16 KB |
参考题解
1 |
|
第二场
M Dirty Work
It is another ICPC contest. Your teammates sketched out all solutions to the problems in a fraction of a second and went away to celebrate, but now you are stuck at implementing them!
There are $n$ problems in total, the $i$-th of which will take $a_i$ seconds to implement. You have the flexibility to choose any unsolved problem to implement, either at the beginning of the contest or right after solving the previous problem.
The total penalty is calculated in a similar manner to ordinary ICPC contests. If you submit and pass problem $i$ at time $ti$, the total penalty is $\sum {i = 1}^{n}t_i$. Note that unsuccessful submissions are omitted from penalty calculations for the sake of convenience.
After completing the implementation of a problem, you will submit it immediately. However, there is a probability $p_i$ that your code for the $i$-th problem fails. In such cases, it will take additional $b_i$ seconds to fix and re-implement the code, and you must address the issue promptly without switching to another problem. It is guaranteed that the second attempt will always succeed.
Now you wonder what the minimal expected total penalty is if you employ an optimal strategy for selecting the next problem to implement.
Input
The first line contains a positive integer $T (1≤T≤10^4)$, denoting the number of testcases.
For each testcase:
- The first line contains one integer n $(1≤n≤5000)$, denoting the number of problems.
- The following n lines each contain two integers $a_i$ and $b_i (1≤a_i,b_i≤104)$, as well as one decimal number $p_i (0≤p_i≤1)$. These values represent the time required for the first and second attempts, respectively, as well as the probability of failure for the first attempt. The decimal number pi has exactly one decimal place.
It is guaranteed that $\sum n≤10^6$, and $\sum_{i = 1}^{n}(a_i+b_i)≤18000$ for each testcase, so that you can always solve all problems in five hours.
Output
For each testcase, print one decimal number, denoting the minimal expected total penalty if you employ an optimal strategy for selecting the next problem to implement. The answer will be considered correct if its absolute or relative error is less than $10^{−9}$.
Sample Input
1 | 3 |
Sample Output
1 | 34.000000000000 |
Notes
In the first test case, you should tackle problem 3 first, followed by problem 2, and finally problem 1.
1 | 代码长度限制 64 KB |
参考题解
- 手搓快排
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
using namespace std;
const int N = 5010;
double x[N];
void ss(int l, int r)
{
if (l >= r) return;
double y = x[l + r >> 1];
int i = l - 1, j = r + 1;
while(i < j)
{
while (x[++i] > y);
while (x[--j] < y);
if (i < j) swap(x[i], x[j]);
}
ss(l, j), ss(j + 1, r);
}
int main()
{
int t, n, a, b;
double p, T;
cin >> t;
for (int i = 0; i < t; i++)
{
cin >> n;
T = 0;
for (int i = 1; i <= n; i++)
{
cin >> a >> b >> p;
x[i] = a*(1-p)+(a+b)*p;
}
ss(1, n);
for (int i = 1; i <= n; i++)
T += x[i]*i;
printf("%.12lf\n", T);
}
}
- STL
1
D Project Manhattan
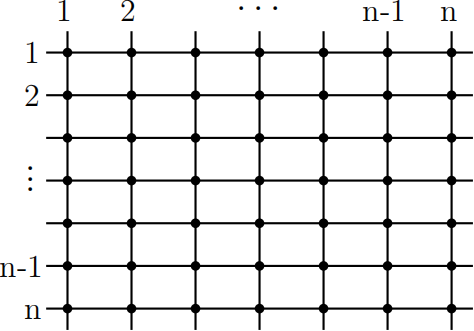
Manhattan consists of n parallel horizontal streets (numbered from 1 to $n$) and $n$ parallel vertical streets (also numbered from 1 to $n$). The streets are perfectly straight, and the horizontal streets are perpendicular to the vertical streets, as shown in the diagram below.
A television station has decided to cover all events happening on the streets of Manhattan. A person standing at the intersection of horizontal street $i$ and vertical street $j$ can see what is happening at all intersections of these two streets with the others. For each intersection, a price has been set for finding a vlogger who is willing to work there (and transmit meaningless news shaking public opinion from both streets they can see). It turned out that for some intersections, this price is negative (some vloggers are willing to pay their employer for publicity). The television station is wondering how to control all intersections and minimize the total fees for vloggers.
Input
The first line of the input contains an integer $T (1≤T≤20)$, denoting the number of test cases.
For each testcase:
The first line of the input contains a positive integer n $(1≤n≤500)$. In the next n lines, there is a description of each horizontal street. The description of one horizontal street contains n numbers separated by single spaces, which are the rental prices for vloggers at the intersections of that street.
It is guaranteed that all prices are in the range $[−10^6,10^6]$.
Output
For each test case, you should print a single integer, denoting the minimum price that the television station must pay to guarantee coverage of all intersections.
Specially, paying a negative price is preferred over a non-negative price.
Sample Input
1 | 2 |
Sample Output
1 | 6 |
1 | 代码长度限制 64 KB |
参考题解
1 |
|